the bend moment M of a beam is given by dm/dx=w(1x) where w and l are constantsdetermine M in terms of x given that M=wl^2/2 plz show me working step Algebra Josephine solved a quadratic equation (x6)^2=49( x2 y2 ) dx 2xy dy = 0 ⇒dydx = y2 x22xy (1)It is a homogeneous differential equationLet y = vx (2) ∴dydx = v xdvdx (3) Substituting (2) and (3) in (1), we get v xdvdx = v2 x2 x22x vxv xdvdx = x2 (v2 1 )2vx2 = v2 12v2v2 2vx dvdx = v2 1 2vx dvdx = v2 12vv2 1 dv = dxx Integrating both sides, we get ∫2vv2 1 dv = ∫1x dxlog v2 1 = log x log Clog v2 1 =Expert Answer (According to Chegg policy only four subquestions will be answered Please post the remaining in another question) 2 dy/dx = x2y3/ (1x3) => dy (1/y3) = x2/ (1x3) dx Integrating both sides, view the full answer Previous question Next question

Number 5 Please 1 14 Odes Integrating Factors Test For Exactness If Exact Solve If Not Use Homeworklib
(x^2-y^2)dx 2xydy=0 given that y=1 when x=1
(x^2-y^2)dx 2xydy=0 given that y=1 when x=1-Of the highest ordered derivative that appears in the given equation The degree of a differential equation is the degree of the highest ordered derivative treated as a variable I Examples (a) @2u @x2 @2u @y2 = 0 is of order 2 and degree 1 (b) (x2 y2)dx 2xydy = 0 is of order 1 and degree 1 (c) d3x dy3 2 x dx dy 4xy = 0 is of order 3 andAnswer to Solve the Ivp with y(1) = 8 and equation (x^2 y^2)dx 2xydy = 0 By signing up, you'll get thousands of stepbystep solutions to




If Dy Dx X Y X Y And Y 1 1 Then Y 2 Equals
Answer to Solve the differential equation (1x^2)y' 2xy=0 Find solutions for your homework or get textbooks Search I'm at the beggining of a differential equations course, and I'm stuck solving this equation $$(x^2y^2)dx2xy\ dy=0$$ I'm asked to solve it using 2 different methods I proved I can find integrating factors of type $\mu_1(x)$ and $\mu_2(y/x)$If I'm not wrong, these two integrating factors are $$\mu_1(x)=x^{2} \ \ , \ \ \mu_2(y/x)=\left(1\frac{y^2}{x^2}\right)^{2}$$ The differential equations find the particular solution satisfying the given condition x^2dy (xy y^2) dx = 0;
Ex 95, 4 show that the given differential equation is homogeneous and solve each of them ( ^2 ^2 ) 2 =0 Step 1 Find / ( ^2 ^2 ) 2 =0 2xy dy = ( ^2 ^2 ) dx 2xy dy = ( ^2 ^2 ) dx / = ( ^2 ^2)/2 Step 2 Putting F (x, y) = / and finding F ( x, y) F (x, y) = ( ^2 ^2)/2 F ( x, y) = ( ( )^2 ( )^2)/ (2 )= ( ^2 ^2 ^2 ^2)/ ( ^22 )= ( ^2 ( ^2 ^2))/ ( ^22 ) = ( ^2 ^2)/2 = F (x, y) F ( x, y) = F (x, y) = F (x, y) Q The curve satisfying the differential equation , (x 2y 2) dx 2xy dy = 0 and passing through the point (1,1) is (a) an ellipse (b) a hyperbola (c)Free exact differential equations calculator solve exact differential equations stepbystep
(x 2 y 2) dx 2xydy = 0 It is a homogeneous differential equation Let y = vx(2) Substituting (2) and (3) in (1), we get Integrating both sides, we get It is given that when x = 1, y = 1 (1) 2 (1) 2 = C(1) C = 2 Thus, the required solution is y 2 x 2 = 2x OR It is a homogeneous differential equation Let y = vx(2)Uploaded By SicilianPenguin Pages 22 This preview shows page 16 out of 22 pages Solve the differential equation x(y1) dx(x1)dy=0 If y=2 when x=1 Latest Problem Solving in Differential Equations More Questions in Differential Equations Online Questions and Answers in Differential Equations




2 Pdf Equations Elementary Mathematics



Solved Solve The Following Ordinary Differential Equation X2 Y2 Dx 2xy Dy 0 Find A Vector That Is Orthogonal To The Plane Containing The Points Course Hero
The equation is a homogeneous equation Let y= vx, Differentiat ing wrt x, we get, `dy/dx=vx (dv)/dx` `dy/dx= (x^2y^2)/ (2xy) " from " (i)` `vx (dv)/dx= (x^2 (vx)^2)/ (2x (vx))` `vx (dv)/dx= (1v^2)/ (2v)` `x (dv)/dx= (1v^2)/ (2v)v` `x (dv)/dx= (1v^22v^2)/ (2v)`Solve the following differential equation (x2−y2)dx2xydy=0 given that \ ( y = 1 \) when \ ( x = 1 \) awsanket1176 is waiting for your help Add your answer and earn pointsSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib



X Y 2 Dx 2xy Dy 0 Sarthaks Econnect Largest Online Education Community
Divide by x* (1y) and multiply by dx to get dy/ (1y)=dx/x and integrate both sides to get log (1y)=log (x)k1 then exponentiate to get 1y=k2*x so y=k2*x1 From this, dy/dx=k2 so x*dy/dx=x*k2=k2*x=1y=1k2*x1=k2*x which verifies the solution y=k2*x1 6 views1/2 (a) Find all equilibrium solutions (Your answer may depend on a) (b) Classify the equilibrium points using the linearization methodClick here👆to get an answer to your question ️ Solve the differential equation (x^2 y^2) dx 2xydy = 0



1




If Dy Dx X Y X Y And Y 1 1 Then Y 2 Equals
SolutionShow Solution Given ( x2 − yx2 ) dy ( y2 x2y2 ) dx = 0 Dividing both the sides by \ dx\, we get \ \left ( x^2 y x^2 \right)\frac {dy} {dx} \left ( y^2 x^2 y^2 \right) = 0\ \ \Rightarrow x^2 \left ( 1 y \right)\frac {dy} {dx We can rearrange this Differential Equation as follows dy dx = − x2 y2 x2 − xy = − ( 1 x2)(x2 y2) ( 1 x2)(x2 −xy) = − 1 ( y x)2 1 − y x So Let us try a substitution, Let v = y x ⇒ y = vx Then dy dx = v x dv dx And substituting into the above DE, to eliminate y Solve (y√(x^2y^2))dxxdy=0 Latest Problem Solving in Differential Equations More Questions in Differential Equations Online Questions and Answers in Differential Equations




Solving Differential Equation 2xy Dy Dx Y 2 X 2 0 Youtube



Show That The Given Differential Equation Is Homogeneous X 2 Y 2 Dx 2xy Dy 0 Sarthaks Econnect Largest Online Education Community
Consider the family of nonlinear systems with parameter a given by dx/dt= x ay dy/dt= 4x2ay Suppose throughout that a >Calculus Find dy/dx y^2=1/ (1x^2) y2 = 1 1 − x2 y 2 = 1 1 x 2 Differentiate both sides of the equation d dx (y2) = d dx ( 1 1−x2) d d x ( y 2) = d d x ( 1 1 x 2) Differentiate the left side of the equation Tap for more steps Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation History




Solve Dy Dx X 2 3y 2 2xy Youtube




2xy Dy Dx X 2 3y 2 Youtube
Solve ( x 2 y 2) dx 2xy dy = 0, given that y = 1, when x = 1 The answer given in the book is x 2 y 2 = 2xSolve the differential equation (x^2 y^2)dx 2xy dy = 0 ;The equation 2xydy (x^2 y^2 1)dx =0 can be rewritten as dy/dx y/2x = (1x^2)/2xy which is a Bernoulli equation To reduce it to normal form take y = U (x)^1/2 Then y' = (1/2) (U^1/2)U' and the equation becomes U' U/x = (1x^2)/x The integrating factor is 1/x and the solution is given




Number 5 Please 1 14 Odes Integrating Factors Test For Exactness If Exact Solve If Not Use Homeworklib




Doc Iii Exact Differentia Equation Joshua Pascual Academia Edu
Given that y = 1 when x = 1 12th Maths Ex 95, 12 For each of the differential equations in Exercises from 11 to 15 , find the particular solution satisfying the given condition 𝑥2𝑑𝑦 𝑥𝑦 𝑦2 𝑑𝑥=0;𝑦=1 When 𝑥=1 The differential equation can be written 𝑎s 𝑥2𝑑𝑦 = −(xy y2) dx 𝑑𝑦𝑑𝑥 = − 𝑥𝑦 𝑦2 𝑥2 LetSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




X 1 Y2 Dx Y 1 X2 Dy 0 Brainly In




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The
Example 1 a If x 2 y 2 25 find dy dx b Find an equation of the tangent to the Example 1 a if x 2 y 2 25 find dy dx b find an School University of the Philippines Baguio;Find the corresponding particular solution for {eq}\displaystyle (x^2y^2)\ dx 2xy\ dy=0 {/eq} using the integrating factor Using an Integrating Factor The given equation is in the form of murshid_islam said If the boundary condition was , both and would be correct solutions, right?



2
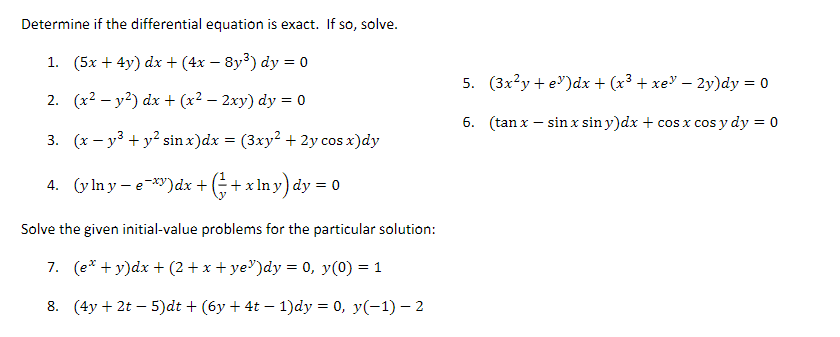



Determine If The Differential Equation Is Exact If Chegg Com
The differential equation is not well defined in (x,y) = (1,1) as you have an expression of the form 0/0 for dy/dx #8 murshid_islamY = 1 when x = 1 asked in Differential Equations by KumkumBharti ( 539k points)The solution of (dy/dx) = (x2 y2 1/2xy), satisfying y (1 Q The solution of d y d x = x 2 y 2 1 2 x y, satisfying y ( 1) = 0 is given by VITEEE VITEEE 14 Differential Equations Report Error A



Solve The Following Differential Equation X2 Y2 Dx 2xy Dy 0 Given That Y 1 When X 1 Or Solve The Following Differential Equation If Y 1 When X 1 Mathematics Topperlearning Com 237hoo



X2 Y2 Dx 2xy Dy 0 3 Search For A Good Cause
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history y^2 = x^2(2lnx c) We can rewrite this Ordinary Differential Equation in differential form (x^2 y^2) \ dx xy \ dy = 0 A as follows \ \ \ \ dy/dx = (x^2 y^2)/(xy) dy/dx = x/y y/x B Leading to a suggestion of a substitution of the form u = y/x iff y = ux And differentiating wrt x whilst applying the product rule dy/dx = u x(du)/dx Substituting into the DE BCourse Title MATH 53;



1




Solve The Differential Equation X2 Y2 Dx 2xydy 0 Given Y 0 X 1 Maths Differential Equations Meritnation Com
Factor out the Greatest Common Factor (GCF), 'dx' dx(1 y 2 1x 2) = 0 Subproblem 1 Set the factor 'dx' equal to zero and attempt to solve Simplifying dx = 0 Solving dx = 0 Move all terms containing d to the left, all other terms to the right Simplifying dx = 0 The solution to this equation could not be determined Solve the following differential equation (x^2 y^2 ) dx 2xy dy = 0 given that y = 1 when x = 1 Sarthaks eConnect Largest Online Education Community Given equation can be written as, ydx xdy2xy²dx x²ydy=0 Dividing both side by (xy)², we get d(xy)/(xy)² 2dx/x dy/y=0 Now it can be integrated easily



Solve The Following Differential Equation X2 Y2 Dx 2xy Dy 0 Given That Y 1 When X 1 Or Solve The Following Differential Equation If Y 1 When X 1 Mathematics Topperlearning Com 237hoo
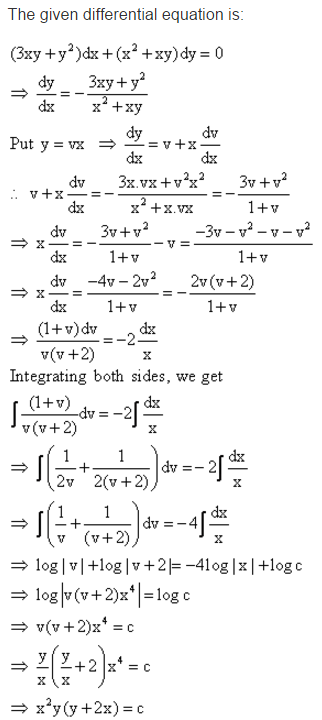



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633
Solution for (2xy)dx (x^21)dy=0 equation Simplifying (2xy) * dx (x 2 1) * dy = 0 Remove parenthesis around (2xy) 2xy * dx (x 2 1) * dy = 0 Multiply xy * dx 2dx 2 y (x 2 1) * dy = 0 Reorder the terms 2dx 2 y (1 x 2) * dy = 0 Reorder the terms for easier multiplication 2dx 2 y dy (1 x 2) = 0 2dx 2 y (1 * dy x 2 * dy) = 0 Reorder the terms 2dx 2 y (dx 2 y 1dy) = 0 2dx 2 y (dx 2 y 1dy) = 0 Combine like terms 2dx 2 y dxSolution for Solve dy/dx=2xy/(x^2y^2) Q A group of 150 tourists planned to visit East AfricaAmong them, 3 fall ill and did not come, of th A Consider the provided question, First draw the Venn diagram according to the given question, Let K rPopular Problems Calculus Find dy/dx 2xyy^2=1 2xy − y2 = 1 2 x y y 2 = 1 Differentiate both sides of the equation d dx (2xy−y2) = d dx (1) d d x ( 2 x y y 2) = d d x ( 1) Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of 2 x y − y 2 2 x y y 2 with respect to x x is d d x 2




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube




X 2 Y 2 Dx 2xydy 0 Cloebeautifull
Solve both parts a and b as they are related Solve the given exact differential equations help_outline Image Transcription close (A) (xy)* dx (2xy x² –1)dy = 0, y (1) =1 fullscreenLearn how to solve differential equations problems step by step online Solve the differential equation xy*dx(1x^2)dy=0 Grouping the terms of the differential equation Group the terms of the differential equation Move the terms of the y variable to the left side, and the terms of the x variable to the right side Simplify the expression \frac{1}{y}dy Integrate both sides of the Get an answer for 'solve the differential equation (2xy3y^2)dx(2xyx^2)dy=0 ' and find homework help for other Math questions at eNotes




Solve The Following Differential Equation X2 Y2 Dx 2xydy 0 Given That Y 1 When X 1 Brainly In
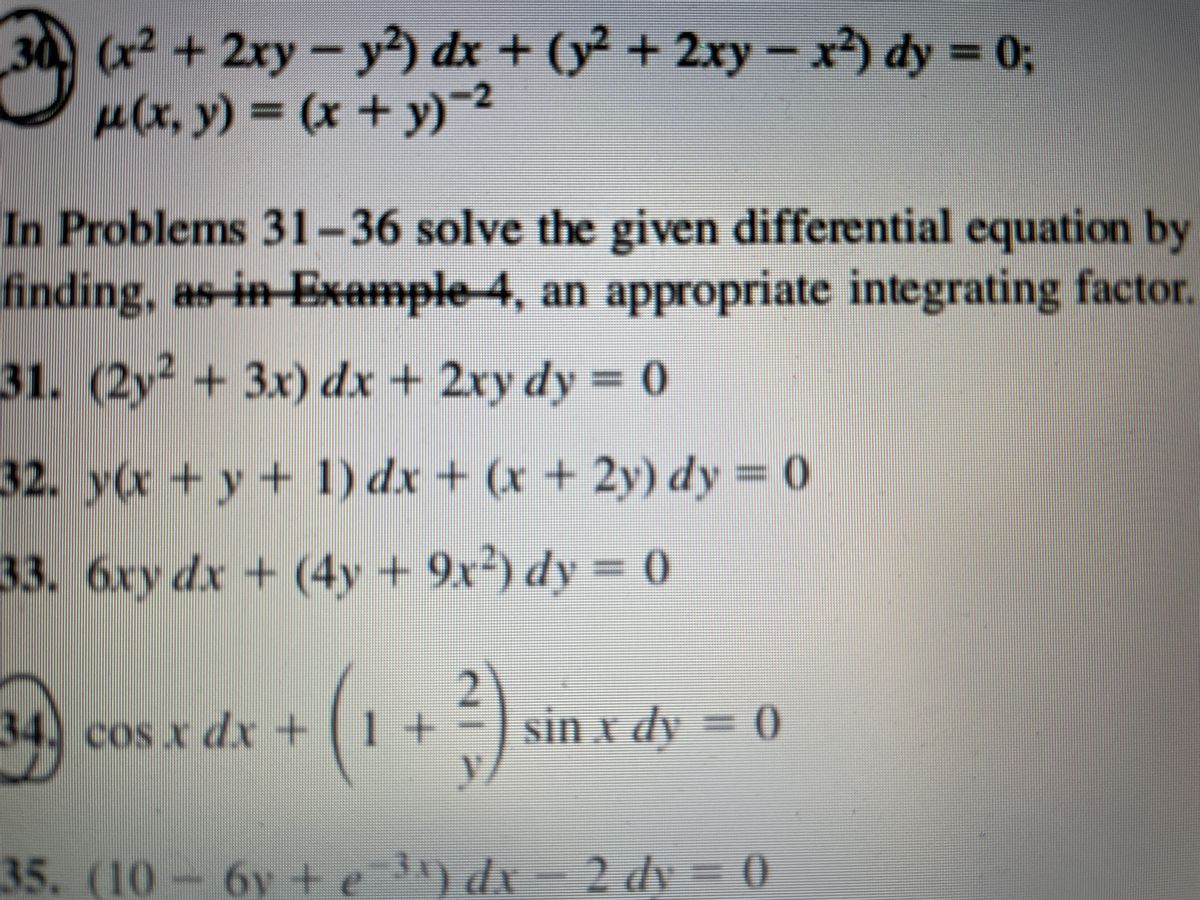



Answered In Problems 31 36 Solve The Given Bartleby
(b) 2 x y dx ( y 2 x 2) dy = 0 Here, M = 2 x y, M y = 2x, N = y 2 x 2, and N x = 2 xNow, ( N x M y) / M = ( 2 x 2 x ) / ( 2 x y) = 2 / yThus, μ = exp ( ∫ 2 dy / y ) = y2 is an integrating factor The transformed equation is ( 2 x / y ) dx ( 1 x 2 y2) dy = 0 Let m = 2 x / y, and n = 1 x 2 y2Then, m y = 2 x y2 = n x, and the new differential equation is exact



Www Selfstudys Com Uploads Pdf Fshc9vrqbhcps1alayff Pdf




X2 Y2 Dx 2xydy 0 Brainly In
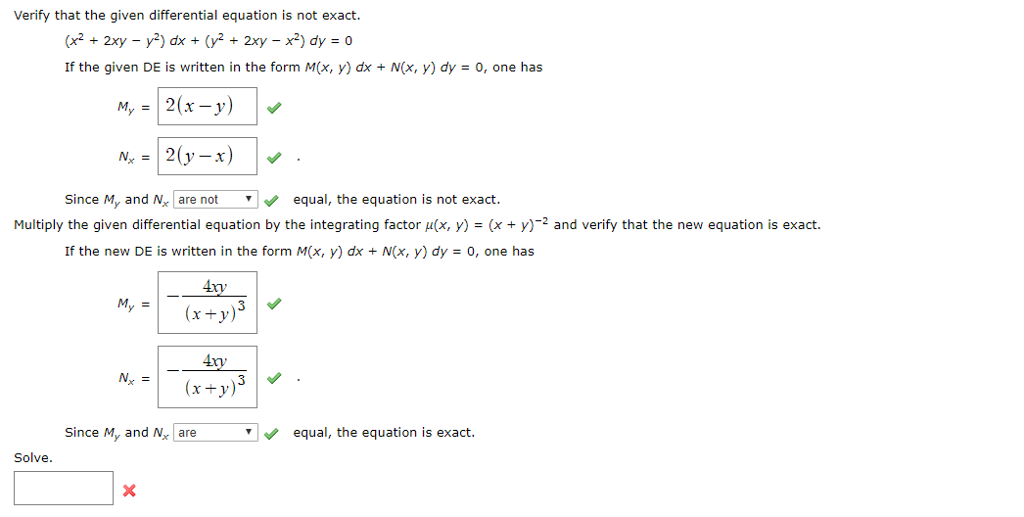



Verify That The Given Differential Equation Is Not Chegg Com




Answered 1 Dt2 K X 0 2 Ax 3 X Y Dx Bartleby



Q Tbn And9gct1xcwysznvpynv5mvjvjxzxdbb8krwtggqfbizpwohngm6uwky Usqp Cau




Vector Analysis By Alimkanwalimtinaa Issuu
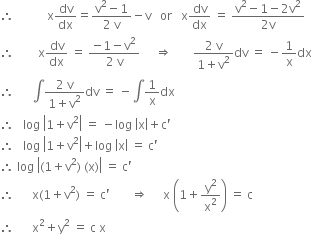



Show That The Given Differential Equation Is Homogeneous And Solve It X2 Y2 Dx 2xy Dy 0given That Y 1 When X 1 Zigya



How To Solve X Y Dx 2xy Dy 0 Quora




Answered A In Each Of Problems 1 Through 10 Bartleby
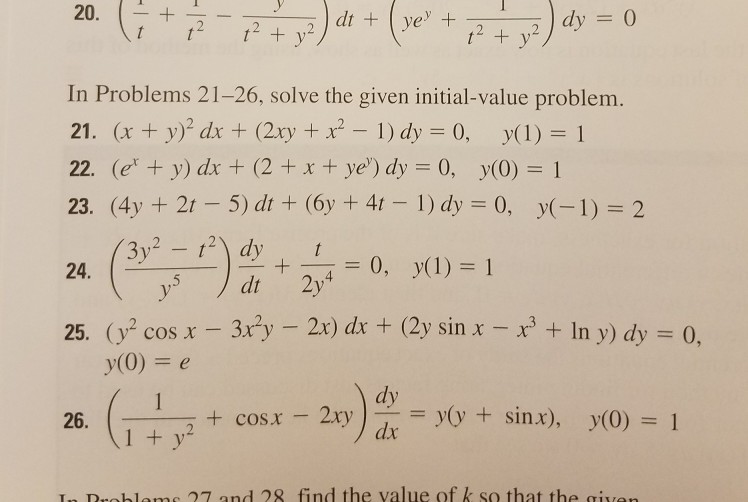



In Problems 21 26 Solve The Given Initial Value Chegg Com
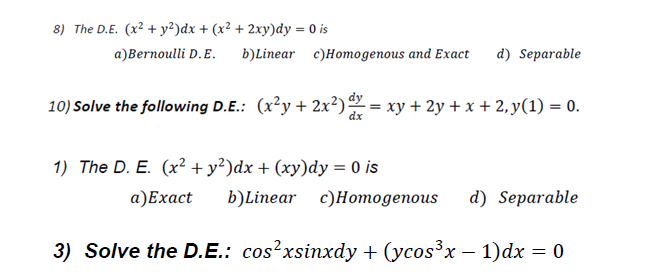



The D E X 2 Y 2 Dx X 2 2xy Dy 0 Is Chegg Com




Solve The Differential Equation X 2 Y 2 Dx 2xydy 0



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q4 Pdf




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5



Solve X 2 Y 2 Dx 2xy Dy 0 Sarthaks Econnect Largest Online Education Community




X 2 Y 2 Dx 2xy Dy 0 The Solution To This Differential Equation Represents Which Curve




02b First Order First Degree Homogeneous Studocu



Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero




Ma 104 Differential Equations




Pomogite Pozhalujsta Srochnr X 2 3y 2 Dx 2xydy 0 Y 2 1 Shkolnye Znaniya Com



Find The Equation Of A Curve Passing Through Origin And Satisfying The Differential Equation 1 X 2dy Dx 2xy 4x2 Studyrankersonline



X2 Y2 Dx 2xydy Search For A Good Cause



2



How To Solve This Differential Equation 2xydy X 2 Y 2 1 Dx 0 Quora




Evaluate X 2 3y 2 Dx 2xy Dy 0 Y 2 6 Study Com




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5



What Is The Solution To 3 3x 2 Y 2 Dx 2xydy 0 Quora




How To Find Exact Equation Quick And Easy Differential Equations Explained Right Youtube



Solved Solve The Homogeneous Differential Equation X2 Y2 Dx 2xy Dy 0 Course Hero




In Solve The Given Initial Value Problem X Y 2 Chegg Com




Engineering Mathematics Notes




Homogeneous Equations



Www Uplifteducation Org Cms Lib Tx Centricity Domain 273 Diff eq sol Pdf




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5



What Is The Solution To This Differential Equation X 2 Y 2 1 Dx X X 2y Dy 0 Quora




1 Given The Differential Equation X2 2xy Y2 Dx Y Chegg Com



Solved Solve The Homogeneous Differential Equation X2 Y2 Dx 2xy Dy 0 Course Hero




For The Differential Equations Find The Particular Solution Satisfying The Given Condition 2xy Y 2 2x 2 Dy Dx 0 Y 2 When X 1 Mathematics Shaalaa Com




Differential Equations Module By Jessarina Olbes Issuu
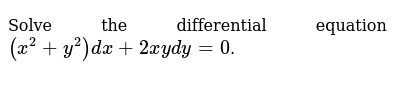



Solve The Differential Equation X 2 Y 2 Dx 2xydy 0




Math 432 Hw 2 5 Solutions




Exact Equations Example 3 Video Khan Academy



Solve The Differential Equation X2 1 Dy Dx 2xy 1 X2 1 Studyrankersonline




Solve The Differential Equation X 2 Y 2 Dx 2xydy 0 Youtube




9 A Show That X X2 Y2 1 Is An Integrating Fac Math




Solve X 2 Y 2 Dx 2xydy 0 Given That Y 1 When X 1 Pls Check The Ans Maths Differential Equations Meritnation Com



1




Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy




Math 432 Hw 2 5 Solutions




Solved Evaluate C X 2 Y 2 Dx 2xy Dy On The Given Closed Curve C 1 Answer Transtutors




Exact Non Differential Equation



Solve The Following Differential Equation X 2 Y 2 Dx 2xy Dy 0 Given That Y 1 When X 1 Sarthaks Econnect Largest Online Education Community



Solve The Following Differential Equation X2 Y2 Dx 2xy Dy 0 Given That Y 1 When X 1 Or Solve The Following Differential Equation If Y 1 When X 1 Mathematics Topperlearning Com 237hoo



X2 Y2 Dx 2xy Dy 0 3 Search For A Good Cause




Number 5 Please 1 14 Odes Integrating Factors Test For Exactness If Exact Solve If Not Use Homeworklib




15 The Differential Equation 2xy Dy X2 Y2 1 Dx Determines A A Family Of Circles With Centre On X Axis B A Family Of Circles With Centre On Y Axis




Miscellaneous Problems Differential Equations



Www Tau Ac Il Levant Ode Solution 6 Pdf




Solution Of The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Is Youtube




Solve The Differential Equation X 2 Y 2 Dx 2xydy 0




Solve Q Solve The Differential Equation X2 Y2 Dx Maths Differential Equations Meritnation Com




If 2xydy X 2 Y 2 1 Dx Y 1 0 And Y X 0 Sqrt3 Then X 0 Ca




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5




Handouts Differential Equation And Advanced Mathematics Determinant Matrix Mathematics




Show That The Given Differential Equation Is Homogeneous And Solve Each Of Them X2 Y2 Dx 2xy Dy 0 Mathematics Shaalaa Com




406 Mathematics Exercise 9 5 On Is Homogen 17 Which In Each Of The Exercises 1 To




Solve The Following Differential Equations Use Chegg Com




Unit 03 Differential Equations Equations Trigonometric Functions




Math 432 Hw 2 5 Solutions Pdf Free Download




The Total Differential Equation Y 2z Y 3 X 2y Dx X 2z X 3 Xy 2 Dy X 2y Xy 2 Dz 0 Mathematics Stack Exchange



How To Solve The Differential Equation X Y Dx 2xydy 0 Quora




Solving Separable Differential Equations Calculus Socratic




How To Solve This Differential Equation 2xydy X 2 Y 2 1 Dx 0 Quora




Math 432 Hw 2 5 Solutions Pdf Free Download




Ex 9 5 4 Show Homogeneous X2 Y2 Dx 2xy Dy 0 Ex 9 5




4 Solve The Exact Differential Equation 1 2xy Dx 4y3 X2 Dy 0 4 Solve The Exact Differential Equation Homeworklib




X 2 Y 2 Dx 2xydy 0 Cloebeautifull



X 2 Y 2 Dx 2xydy 0 Cloebeautifull



0 件のコメント:
コメントを投稿