U = π (r 2 − h 2)球の体積を求める公式は、V = 4/3 πr^3 で表されます。 このページでは、例題と共に、この公式の使い方を説明しています。 お使いのブラウザでは JavaScript が無効になっています。正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積

中学数学 球の体積の何で 数樂管理人のブログ
球体の体積の求め方
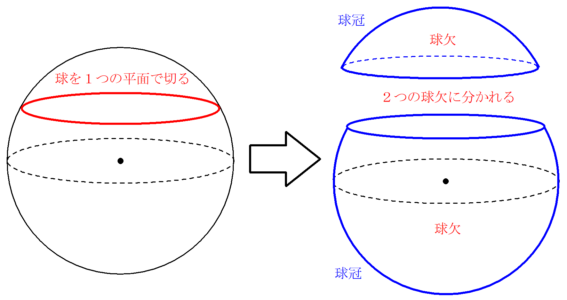
球体の体積の求め方-280 · 球を1つの平面で切り取った部分である球欠について考えます。凸レンズの体積を求める際にも利用できます。 Ⅰ 球欠と球冠とは? Ⅱ 球欠の体積 Ⅲ 球冠の面積 Ⅰ 球欠と球冠とは? 言葉として · 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張
· 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱球の体積の求め方を忘れていたので活用させていただきました。 1149 女/歳代/会社員・公務員/非常に役に立った/ 使用目的 球体の24金の体積を求めるのに使用しました。 1034 女/歳代/主婦/役に立った/ 使用目的6321 · 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4 π r 2 →「心配アール二乗」 球の体積: 4 3 π r 3 \dfrac{4}{3}\pi r^3 3 4 π r 3 →「身の上に心配アール三乗」 表面積は半径の二乗に比例し,体積は半径の三乗に比例することは感覚的に明らかです。
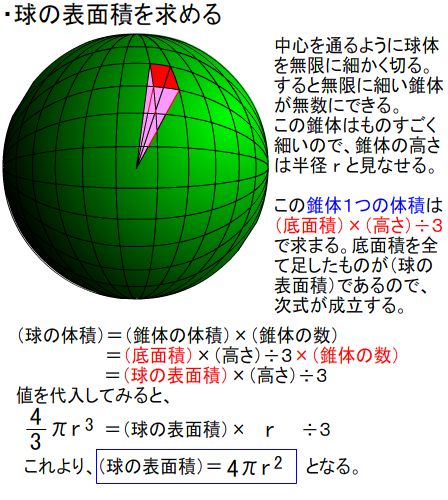
教育現場の先生方に役立つ、授業のヒント。 教育現場で使えるアイディアが盛りだくさんのカシオ計算機の教育情報サイト。 関数電卓 例題と操作 地球の 体積を 求めて みよう①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r218 · 円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!←今回の記事
141 · 球体の表面積S = 4πr 2 目標: 積分 を用いて上式を導出する 方法を2つ考えました. 求め方1:微笑の範囲を考える方法 求め方2:球体の体積を用いる方法6321 · 底面の半径が r 1 r_1 r 1 ,天面の半径が r 2 r_2 r 2 ,高さが h h h である球台の体積は, V = 1 6 π h ( 3 r 1 2 3 r 2 2 h 2 ) V=\dfrac{1}{6}\pi h(3r_1^23r_2^2h^2) V = 66916 · 1:球の体積の求め方(公式) まずは球の体積の求め方(公式)を紹介します。 下の図のように、 半径rの球があるとき、球の体積は4πr 3 / 3 となります。



Q Tbn And9gcqwkabdudclaf 47vgw O93wu16c0ercc O5o6eo6xp177ses0w Usqp Cau




球の表面積の求め方 その3 感じる科学 味わう数学
· 今回は、球の体積・表面積の求め方(公式)について書いていきたいと思います。 球の体積の求め方公式 球の表面積の求め方公式 球の体積・球の表面積を求める問題 問題① 《球の体積の求め方》 《球の表面積の求め方》 問題② 《球の体積の求め方》 《球の表面積の求め方》 問題球の表面積の求め方 公式と計算例 Scipursuit 表面積の求め方 球 球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。 球の表面積を求めるには、この公式に球の半径 r を代入体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方
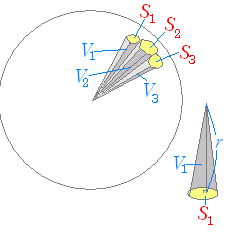



例題対比 球の体積と表面積



Yogb6 Tjpto Wm
141 · 球の体積V = 4 3πr 3初等幾何学における球体は決められた点から決められた距離以内にある点の全体が空間において占める領域であった。 同様のことを n次元ユークリッド空間で行って n次元超球体が定義される。 n次元超球体の体積率 は数学全般を通して現れる重要な定数の一種である。体積 = 一辺 × 一辺 × 一辺




初等幾何 球の表面積を求める 大人が学び直す数学




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
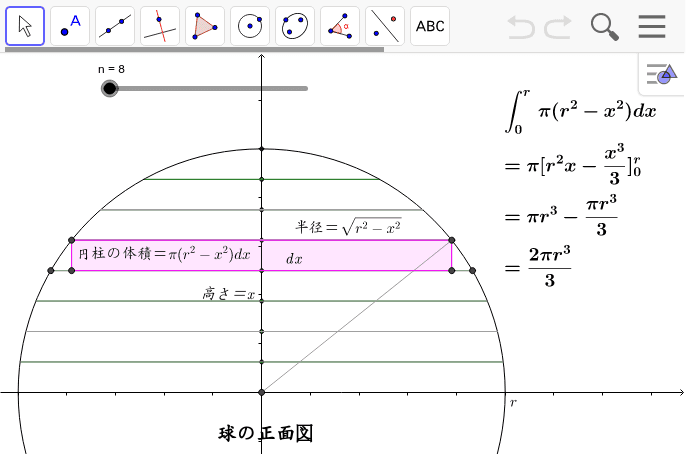
球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積)体積を数値積分で求めることを考えてみましょう。ここでは球の体積を求めること を考えます。 まず、 高校の数学3の復習です。平面に半径1の円を描き、 それをx軸もしくはy 軸について回転させれば、半径1の球が出来上がります。したがって、この性質をの共通部分 の体積 を求めよ. 次 314 曲面積 上 3 多重積分 前 312 演習問題 ~ 多重積分の積分変数の変換 平成21年12月2日



Math 円柱 内接する球 円錐の体積と表面積 働きアリ




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく
半球台の体積 円環体の体積 楕円体の体積 一部が欠けた楕円体の体積 一部が欠けた回転楕円体の体積 正多面体の体積 n次元の球の体積 · 球の体積の求め方 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式にr=5を代入して · その体積の略算式でなるほどと思ったことが・・・。 みなさん、円の面積の求め方ってどのように習いました? 半径×半径×円周率314(ゆとり教育では3だとか)じゃありませんか?



Q Tbn And9gcr6jkoybdanugf1fmicpptzy5auleu32fgwe6 X Jkyzlirf8w1 Usqp Cau




球の体積 球の表面積の公式の導出 積分 優技録
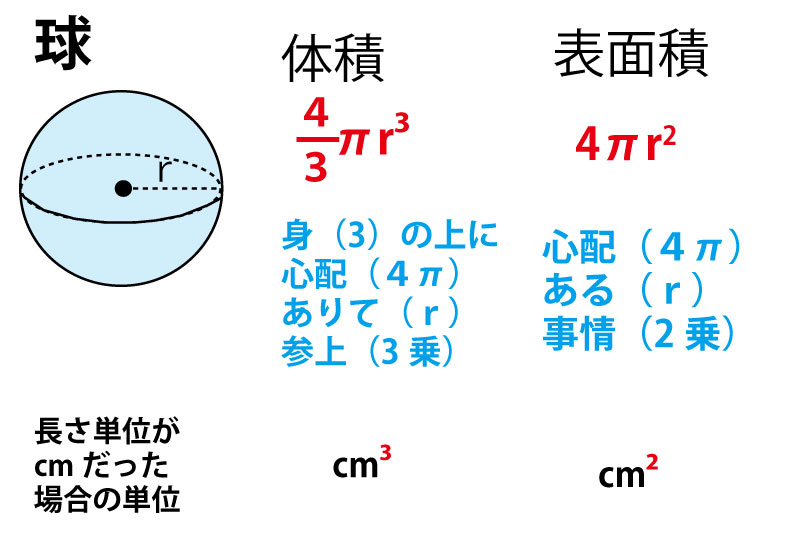
球の体積は \(\dfrac{4}{3}{\pi}r^{3}\) となります。 語呂合わせとして有名なのが、 「身の上に心配あるので参上」 です。 分母の3の上に分子の4があることを「身(3)の上に心(4)~」という言葉で表しており、とても上手い語呂合わせとなっています。 「心配ある」という部分は表面積の公式と球の体積の求め方を簡単に小学生でもわかるように解説をお願いします♪( ´ `) 球体の体積と円の面積についてです。 同じ半径をもつ球体と円があるとします。 このとき、半円の回転体を球体と考えることができます。 だったら、球体を半円が360度回転今回は、球の体積・表面積の求め方(公160 · 優雅 球体 表面積 求め 方 球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説し 中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学び 球の表面積と体積の公式 数学fun 中学数学 球の体積の求め方の公式を1発で覚える方法



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




Mathematics 球の体積と表面積を求める公式 働きアリ
175 · ひどい 球体 体積 求め 方 角錐 円錐の体積と表面積の公式 数学fun 中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru315 · 新しい 球体 体積 求め 方 計算しない方が賢い時がある 苦手な数学を簡単に 中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru球体の体積の求め方を覚える 球体の体積の求め方は「4/3πr 3 」です。 「π」は円周率あるいはパイ、「r」は半径を指します。 例えば「3分の4かけるパイアール3乗」と覚えてしまいましょう。



Sphere 01




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題
V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体球の半径から体積と表面積を計算します。 一部が欠けた球の体積 一部が欠けた球の体積 一部が欠けた球の体積と表面積を計算します。 弓形の回転体の体積 弓形の回転体の体積 弓形の回転体の体積と底面積と表面積を計算します。 · 円錐の体積の求め方の公式 は、 底面積×高さ×1/3



球の体積の求め方とその証明 高等学校で学ぶ積分の知識が必要
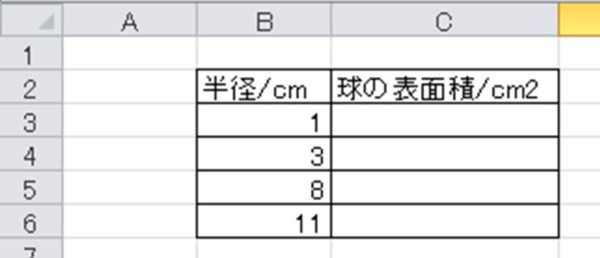



Excel エクセルで球の体積と表面積を計算する方法 モッカイ
· 球の体積の公式 は、 (3分の4)×(円周率)×(半径)×(半径)×(半径) · 何度もすみません。今度は「球体の面積の求め方」を知りたくなりました。(学校で使うので)誰でも良いので、よろしくお願いします。球の面積は、4πr^2 です。(覚え方・・・心配ある事情)ちなみに、体積は、4/3 πr^3(覚え方・・・ · まず、球の体積の定義は体積=4/3 πr^3 となります。 表面積を算出したときと同様に、球の体積も同時に計算していきましょう。 まずは、体積を一気に求めていくために基準となる計算を




球の表面積と体積の求め方 苦手な数学を簡単に
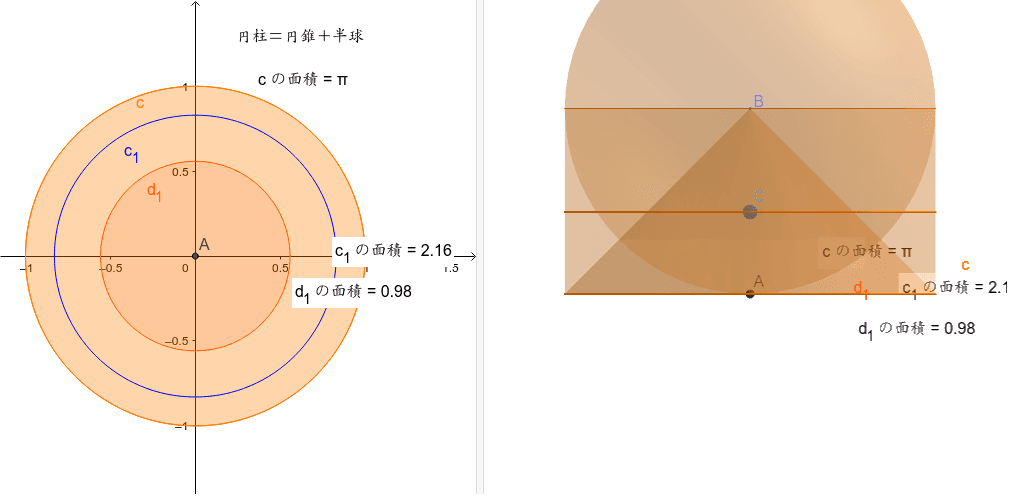



球の体積の求め方 Geogebra




これまでで最高の面積 球 の 体積 の 求め 方 最高のぬりえ



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の体積と表面積の求め方は Peing 質問箱



球の体積 簡単に計算できる電卓サイト



球の表面積の公式の求め方




球の体積と表面積 Jsciencer




球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear




球の体積 表面積 無料で使える中学学習プリント




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




体積の求め方 計算公式一覧



立体 の 表面積 求め 方




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球の体積 表面積 無料で使える中学学習プリント




球体の体積 中学生に分かるように真剣に考えてみた うちーノート




球の表面積 体積 身勝手な主張
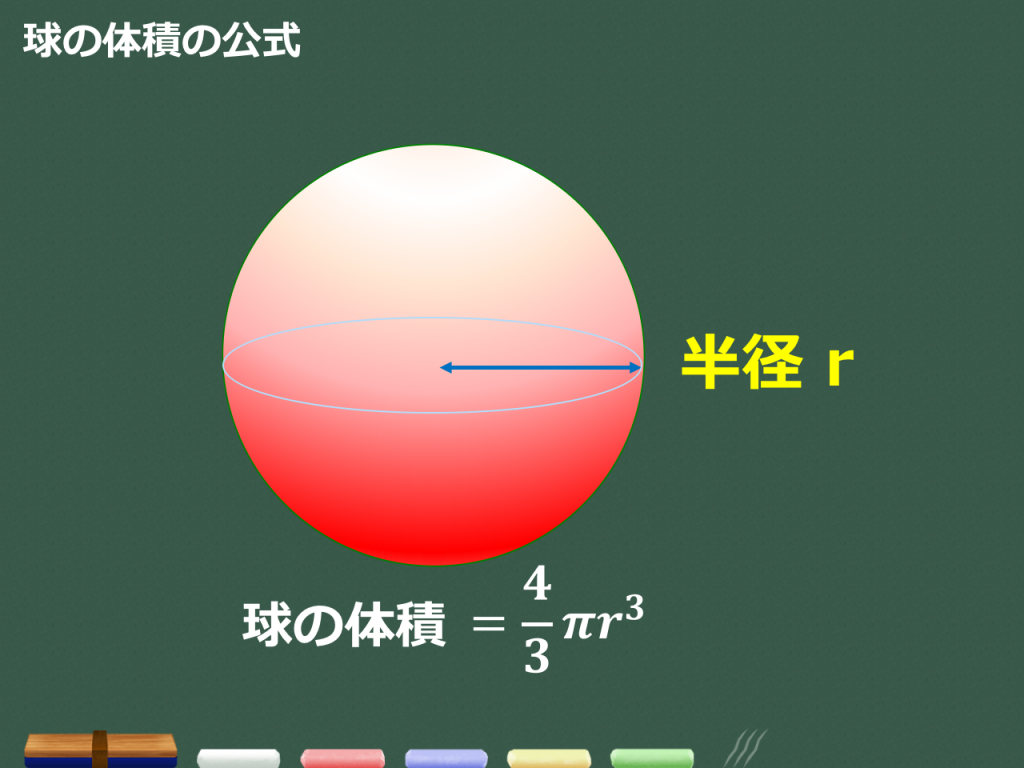



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




中1 数学 中1 84 球について Youtube




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




球冠 Wikipedia



Lh3 Googleusercontent Com Proxy I9sre4qyd3rp7hbcjg2f Cqc14coo1go P9szjuk1pkeb59kofcre Zvhl5vdffcz Mvricxj2x Ksv6f2rm723tvjzc4 N4q9r7y6h9z0zl3zxfgxagyyjk2gkpkd1erharccxk44ymjdoqkdvka3b2cjc1cz9euid5vagksryahu2onbwghgult4khypo Crict7ue9vfwqnthoxvhc29fpnlglknvf5evvcmdju74r Ayxcgy11wudg Qehx8xsberdwwizd Wz60jsfglt Ozhken2lbcrvpfdscmatesls4yq4skmc5yzn5mp1opmb69dx7zibz5vgmfcdqtzyhwtrk Xgnkmxnpy4cml Nrquqrjmwfnjq8bgr




球の表面積と体積の公式 数学fun




中1数学 球 練習編 映像授業のtry It トライイット
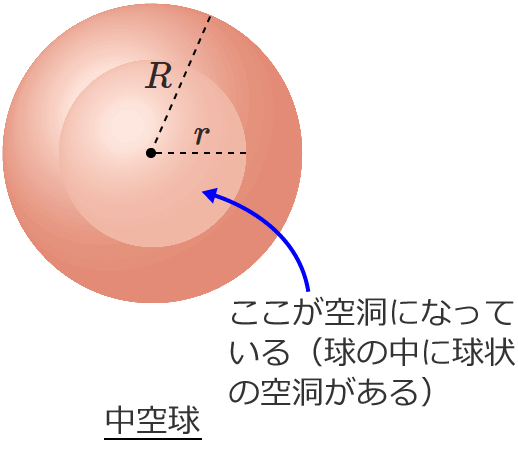



立体の体積を求める公式




球の表面積の求め方 公式と計算例




半球の体積と表面積を計算する 具体例で学ぶ数学



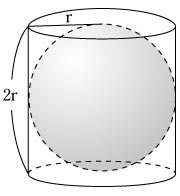
1 この球の体積と円柱の体積の比を求めなさい 2 この球の表面積と円柱の Yahoo 知恵袋
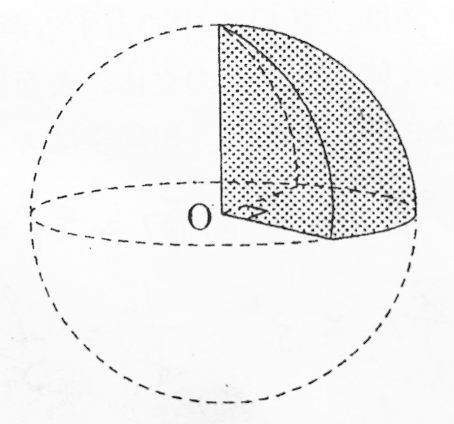



球の問題 苦手な数学を簡単に




中学数学 球の体積の何で 数樂管理人のブログ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球の表面積と体積の公式 数学fun
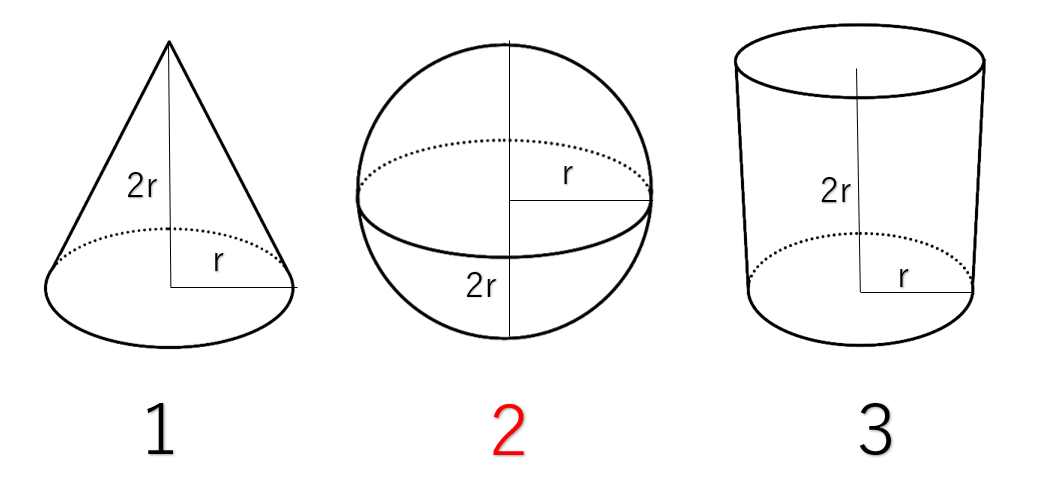



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾




球の表面積と体積の公式 数学fun




球の体積と表面積 数学i フリー教材開発コミュニティ Ftext




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球の体積公式の微分が表面積になっている理由 Youtube
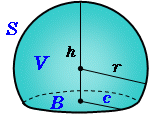



一部が欠けた球の体積 高精度計算サイト




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の体積の求め方 感じる科学 味わう数学



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



研究



数学 球の表面積を積分で計算してもうまくいかない人へ




中1 中一数学 球の表面積と体積 中学生 数学のノート Clear



用語与太話 masa ラボ 鸚鵡 オウム の会議は白昼夢 楽天ブログ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



中1数学 球の表面積と体積の求め方と練習問題 Atstudier




体積とは コトバンク




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




球に関する公式 理数系無料オンライン学習 Kori



Q Tbn And9gcqqgrizekrnz Lytyjejolqml9yfhpazps6kyq0k Jpevu2dxgk Usqp Cau




球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



Search Q E5 86 86 E6 9f B1 81 Ae E4 93 E7 8d Tbm Isch



大学入試問題




球の体積 球の表面積の公式の導出 積分 優技録



球欠と球冠 Fukusukeの数学めも



球の体積の積分 Geogebra




2次元 3次元 4次元 5次元 高次元 の球の体積 宇宙に入ったカマキリ




球の表面積と体積の公式 数学fun




球の体積と表面積 Youtube




球 体積 求め方 ニスヌーピー 壁紙



球の表面積の公式の求め方




中1 数学 6 5 球の体積 表面積 Youtube



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋



Studydoctor球の表面積や体積の公式と求め方 中学1年数学 Studydoctor
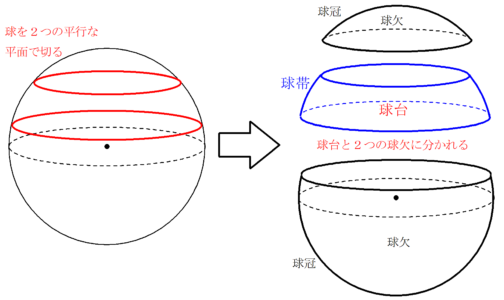



球台と球帯 Fukusukeの数学めも



数学トピックq A
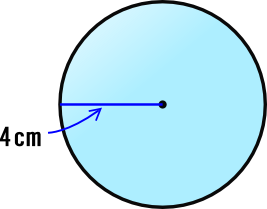



中学1年数学練習問題 球の体積と表面積の求め方と解答 空間図形
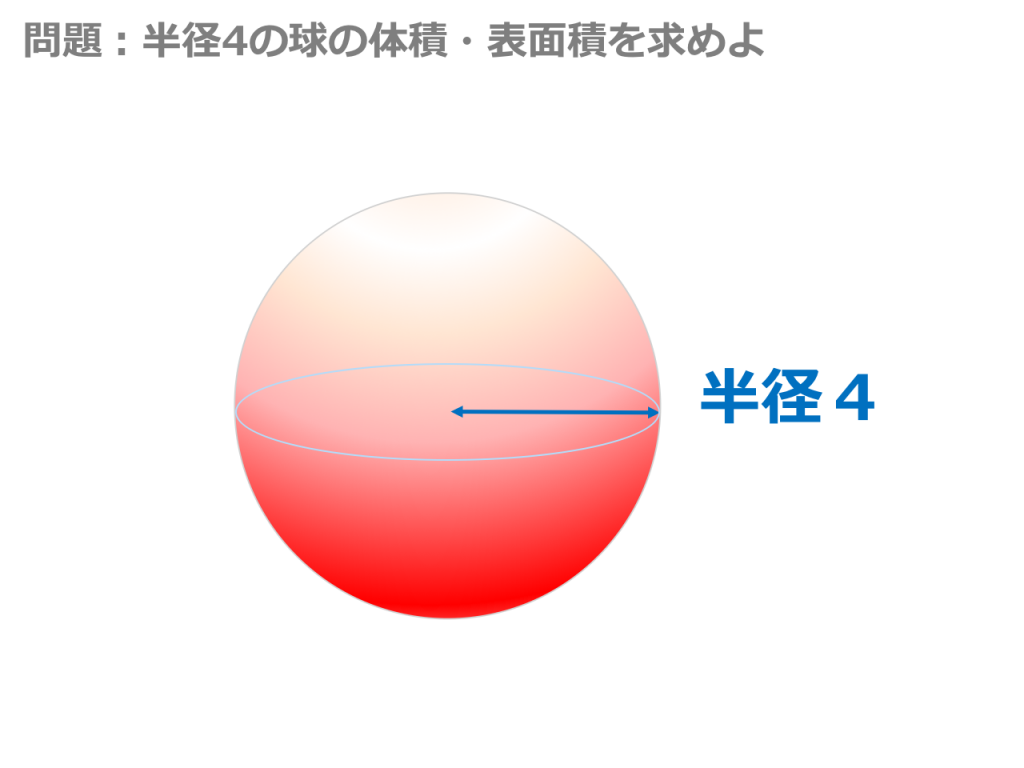



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




球の体積と表面積 公式と計算問題と証明 Irohabook




中1数学 球 例題編 映像授業のtry It トライイット




球の体積の求め方を教えていただけませんか よろしくお願いしますm M Clear



立体の体積を求める公式




球の表面積の公式について みたにっき はてな
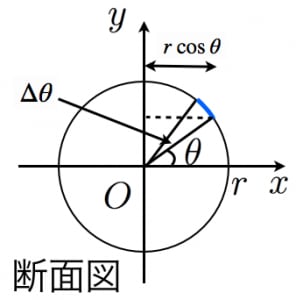



球の体積と表面積を積分で証明 高校数学の美しい物語



0 件のコメント:
コメントを投稿