Since you are differentiating with x;Precalculus Graph y^22yx=0 y2 2y − x = 0 y 2 2 y x = 0 Move all terms not containing x x to the right side of the equation Tap for more steps Subtract y 2 y 2 from both sides of the equation 2 y − x = − y 2 2 y x = y 2 Subtract 2 y 2 y from both sides of the equation Probably you can recognize it as the equation of a circle with radius r = 1 and center at the origin, (0,0) The general equation of the circle of radius r and center at (h,k) is (x −h)2 (y −k)2 = r2 Answer link
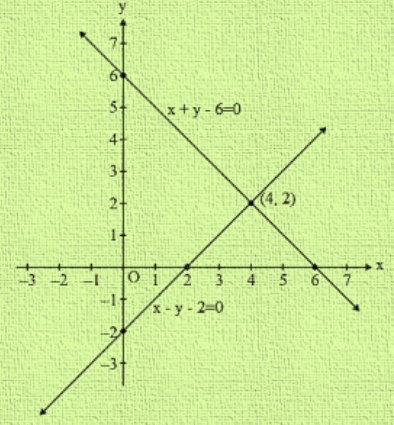
R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
Graph the circle x^2+y^2-14x+2y+41=0
Graph the circle x^2+y^2-14x+2y+41=0- 2x 6y 3 = 0 x^2y^2 = (2x^2 2y^2 x)^2 Differentiating term by term wrt x That means simple x terms differentiate normally but while differentiating those with y;Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Solve The Following Equations Graphically 3x 2y 4 5x 2y 0
Explanation From the given equation x2 y2 2x −3 = 0 perform completing the square method to determine if its a circle, ellipse, hyperbola There are 2 second degree terms so we are sure it is not parabola x2 y2 2x −3 = 0 x2 2x y2 = 〽Graph it yourself !X^{2}3xy^{2}2y=0 Quadratic equations such as this one can be solved by completing the square In order to complete the square, the equation must first be in the form x^{2}bx=c
Solution for x^2y^22y=0 equation Simplifying x 2 y 2 2y = 0 Reorder the terms x 2 2y y 2 = 0 Solving x 2 2y y 2 = 0 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right Add '2y' to each side of the equation x 2 2y 2y y 2 = 0 2y Combine like terms 2y 2y = 0 x 2 0 y 2 = 0 2y x 2 y 2 = 0 2y Remove the zero x 2 1 The equation of a circle is x^2 y^2 4x 2y 11 = 0 What are the center and the radius of the circle?For the region between the graphs of {eq}x= y^2 {/eq} and x= 2y rotated around the line y= 2, find the volume of the resulting solid
x(y5) x(x 2 y 2)(2y) = 0 Subtraction produces 5y 5x = 0 which yields x = y Back substitution produces x 5 2x(2x 2) = 0 4x 3 x 5 = 0 The solutions are x = 1, x = 1/2 i and x = 1/2 i For x=1, y=1, and z=2 The point on the graph of z = x 2 y 2 closest to the point (5,5,0) is (1,1,2) d(1,1) = 6Substitute (y1)2 − 1 ( y 1) 2 1 for y2 2y y 2 2 y in the equation x2 y2 2y = 0 x 2 y 2 2 y = 0 Move −1 1 to the right side of the equation by adding 1 1 to both sides Add 0 0 and 1 1 This is the form of a circle Use this form to determine the center and radius of the circleAnswer to Find the center and radius of the circle x^2 y^2 4x 2y = 0 By signing up, you'll get thousands of stepbystep solutions to your




Which Of The Following Pairs Of Linear Equations Are Consistent Inconsistent If Consistent Obtain The Solution Graphically I X Y 5 2x 2y 10 Ii X Y 8



Graphinglines
Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepYou'll have to multiply those with dy/dx Step by step differentiation x^2y^2 = (2x^2 2y^2 x)^2 2x2y (dy/dx) = 2 (2x^2 2y^2 x)(4x 4y(dy/dx) 1) xShow your work Answer 2 Write the equation of the circle in general form Show your work



The Substitution Method




Solutions To Implicit Differentiation Problems
We want to rewrite \(x^2 y^2 = 2x 2y\) to its standard form \(x^2 y^2 = 2x 2y\\ x^22xy^22y=0\\ x^22x1y^22y1=2\\ (x1)^2(y1)^2=2\) The circle has a center of \((1,1)\) and a radius of \(\sqrt2 \) Largest x value on the circle graph is farthest right, \(\boxed{1\sqrt2}\) If there is any part you don't understand, pleaseAnswered 3 years ago Author has 33K answers and 15M answer views There is no radius because this is not a circle Factorize x^2y^2=0 (xy) (xy)=0 Now because of this, your graph will be where either xy=0, and where xy=0 As you can tell, those are going to be a pair of lines, intersecting at (0,0)Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Solve The Following Equations Graphically 3x 2y 4 5x 2y 0




Omtex Classes 3x 4y 7 5x 2y 0 Solve The Following Simultaneous Equations Graphically
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyUse implicit differentiation to find the points where the parabola defined by {eq}x^22xyy^26x2y13=0{/eq} has horizontal and vertical tangent linesSimple and best practice solution for x^23xy^22y=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework




Draw The Graph For The Following Linear Equations I Y 4 Ii X 2 Iii 2x 4 0 Iv 6 2y 0 V 9 3x 0




Draw Graphs Of The Equation 3x 2y 4 And X Y 3 0 In The Same Graph And Find The Coordinates Youtube
8 MATH PRACTICE TEST FORM 18 32) 31) 33) 34) 9 square yards is a) 1 square foot d) 81 square foot b) 3 square foot e) 243 square foot c) 27 square foot One factor of 3xGraph the function sin(x 2 y 2) yourself for nnulus y 2 – 2y = 0 a = 1, b = 2, c = 0 We need to expand, multiply y with both y and 2 and the output you get is in the desired general form To sketch the graph of f we shift the graph of \(y = x^2\) three units to the proper and two units down If the coefficient of \(x^2\) isn't 1,
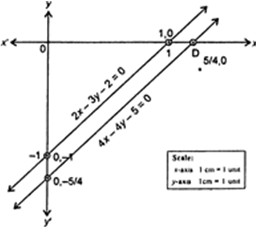



Which Of The Following Pairs Of Linear Equations Are Consistent Inconsistent Consistent Obtain The Solution Graphically 2x 2y 2 0 4x 4y 5 0 From Mathematics



Systems Of Linear Equations
Find an equation of the tangent line to the graph of {eq}y^2(y^24)=x^2(x^24) {/eq} at the point {eq}(0, 2) {/eq} Tangent Line A tangent line is a linear function whose graph intersects a curveCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history Make use of a few conversion formulas and simplify See below Recall the following formulas, used for conversion between polar and rectangular coordinates x^2y^2=r^2 rsintheta=y Now take a look at the equation x^2y^22y=0 Since x^2y^2=r^2, we can replace the x^2y^2 in our equation with r^2 x^2y^22y=0 >r^22y=0 Also, because y=rsintheta, we can replace the




X 2y 0 Graph Novocom Top



How Do You Graph X 2 Y 2 1 Socratic
X^{2}2xy^{2}2y=0 Quadratic equations such as this one can be solved by completing the square In order to complete the square, the equation must first be in the form x^{2}bx=cThe equations are x 2 y 2 2x 2y = 0 and 4x 2 y 2 8x = 0 Find the points of intersection by algebraically Write equation 1 x 2 y 2 2x 2y = 0 in complete square form (x 2 2x) (y 2 2y) = 0 To change the expressions (x 2 2x) and (y 2 2y) into a perfect square trinomial add (half the x or y coefficient)² to each sideThe curves are expressed as functions x ( y) x = y 2 2 y is an upwardfacing parabola x = 3 is a horizontal line above the parabola Plot x = y^2 2y and x = 3 together Find the limits of integration as values of y Set the functions x ( y) equal to each other
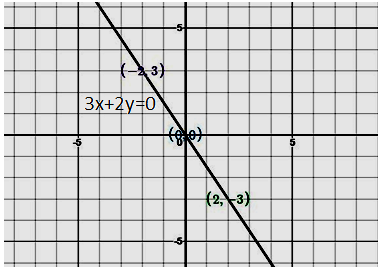



Plot The Line 3x 2y 0 Class 10 Maths Cbse



1
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreApplying the previous theorem gives ZZ D xcosydA = Z 2 0 Z x2 0 xcosydydx = Z 2 0 xsiny x 2 0 dx = Z 2 0 xsin(x2)dx 1 2 cos(x2) 2 0 = 1 2 (1 cos(4)) Example Find the volume of the solid that lies under the elliptic paraboloid z = 3x2 y2 and above the region D bounded by y = x and x = y2 y To nd the points of intersection of these curves, letFrom the origin, chords are drawn to the circle x 2 y 22y = 0 The locus of the middle point of these chords is View solution The equation of a chord of the circle
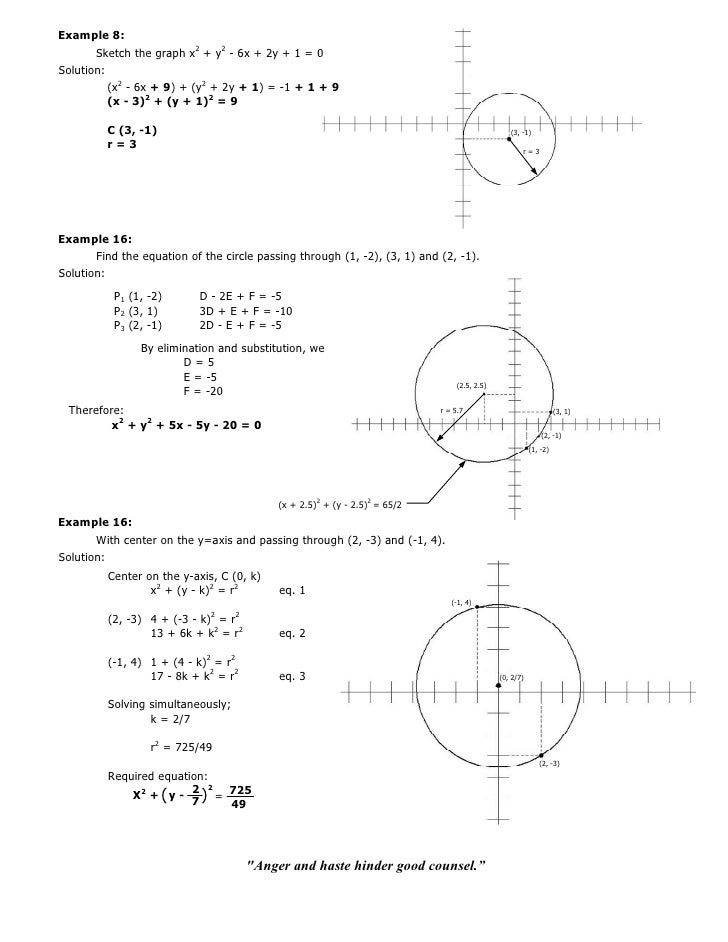



003 Circle




Ex 3 A Q15 X 2y 2 0 2x Y 6 0 Solve Each Of The Following Given Systems Of
Answer to Convert the rectangular equation x^2 y^2 2y = 0 to polar form By signing up, you'll get thousands of stepbystep solutions to yourSolution for y^2(2y)=0 equation Simplifying y 2 (2y) = 0 Reorder the terms (2y) y 2 = 0 Solving (2y) y 2 = 0 Solving for variable 'y' Factor out the Greatest Common Factor (GCF), 'y' y(2 y) = 0 Subproblem 1 Set the factor 'y' equal to zero and attempt to solve Simplifying y = 0 Solving y = 0 Move all terms containing y to the left, all other terms to the rightThe graph of r = 0 is the pole (It represents one point only) The pole is included in the graph of r – 2sin (θ) = 0 We can discard r = 0 and just keep r – 2sin (θ) = 0 r = 2sin (θ) The polar form of x2 y2 – 2y = 0 2 Polar to Rectangular Change r = –3 cos (θ) to rectangular form Solution Use r2 = x2 y2 and x = r cos (θ)




Solution Find The Value Of K For Which The Equation X 2 Y
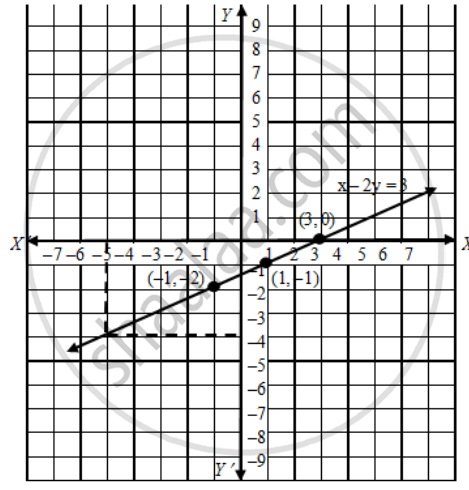



Draw A Graph Of The Line X 2y 3 From The Graph Find The Coordinates Of The Point When I X 5 Ii Y 0 Mathematics Shaalaa Com
Solution for x^2kxy^22y=0 equation Simplifying x 2 1kx y 2 2y = 0 Reorder the terms 1kx x 2 2y y 2 = 0 Solving 1kx x 2 2y y 2 = 0 Solving for variable 'k' Move all terms containing k to the left, all other terms to the right Add '1x 2 ' to each side of the equation 1kx x 2 2y 1x 2 y 2 = 0 1x 2 Reorder the terms 1kx x 2 1x 2 2y y 2 = 0 1x Volume is always V = ∭ d V We just need to set this up You had the right idea of using cylindrical coordinates So thus far we have ∭ r d z d r d θ Notice that for our region, z always 'starts' at the paraboloid and continues up untilFind the Center and Radius x^2y^22x=0 Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Tap for more steps Cancel the common factor of



How To Draw The Graph Of X 2 Y 2 2x 0 Quora
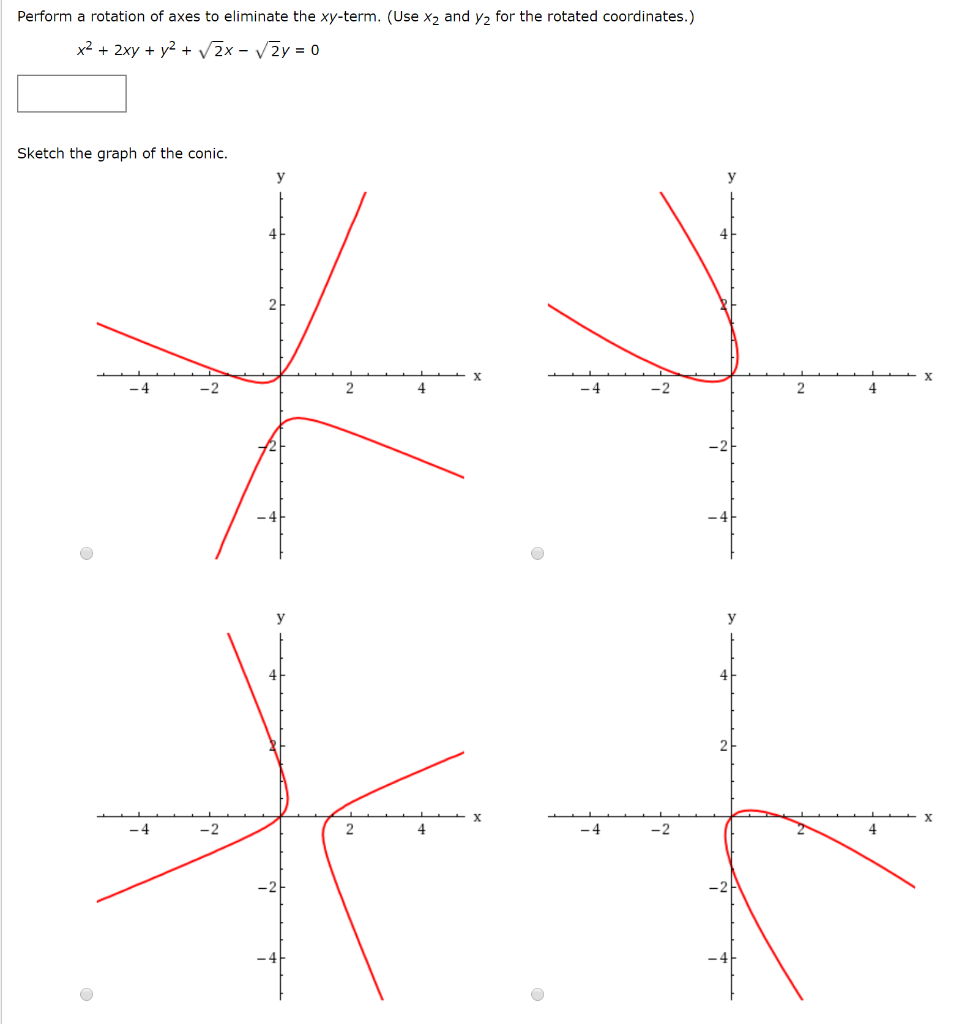



Perform A Rotation Of Axes To Eliminate The Xy Term Chegg Com
PreAlgebra Graph x2y=0 x − 2y = 0 x 2 y = 0 Solve for y y Tap for more steps Subtract x x from both sides of the equation − 2 y = − x 2 y = x Divide each term by − 2 2 and simplify Tap for more stepsAnswer to convert the rectangular equation x^2 y^2 2y=0 to polar form By signing up, you'll get thousands of stepbystep solutions to your graph {x^2y^22sqrt (x^2y^2)2y=0 10, 10, 5, 5} The genera equation of the cardioid is r = a(1 cos(θ −α)), with cusp at the pole and axis of symmetry, along the radial line θ = α Here a = 2 and α = − π 2 Answer link




Minimise And Minise Z 3x 4y Subject To X 2y Le 0 3x Y Le 4 X



Draw The Graphs Of The Equations X Y 1 0 And 3x 2y 12 0 Determine The Coordinates Of The Vertices Of The Triangle Formed By These Lines And The X Axis Mathematics Topperlearning Com 7tnslr9gg
x^2 y^2 = 2x 2y x^2 2x y^2 2y = 0 Complete the square on x and y and we have that x^2 2x 1 y^2 2y 1 = 2 ( x 1)^2 (y 1)^2 = 2 r=2sintheta >Using the formulae that link Cartesian to Polar coordinates • x = rcostheta" and "y=rsintheta and substituting into the given equation rArr(rcostheta)^2(rsintheta)^22rsintheta=0 expanding brackets to obtain r^2cos^2thetar^2sin^2theta=2rsintheta Take out a common factor of r^2Simple and best practice solution for 2xy(4y^2)dx(y1)(x^22)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework



Cbse 9 Math Ncert Solutions
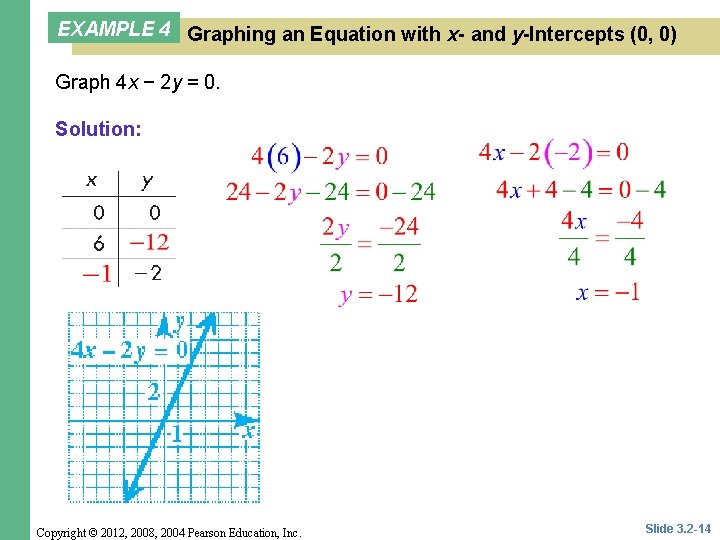



Chapter 3 Section 2 3 2 Graphing Linear
x^2 y^2 = 2y 4sqrt(x^2y^2) Use the conversions r^2 = x^2 y^2 r = sqrt(x^2y^2) rsintheta = y rcostheta = x First, let's multiply both sides of the equation by r r*r = r*(2sintheta4) r^2 = 2rsintheta 4r Now we can substitute the rectangular forms x^2 y^2 = 2y 4(sqrt(x^2y^2)) x^2 y^2 = 2y 4sqrt(x^2y^2) We can simplify this further, but this is aSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreGraph x^22xy^22y=0 Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Tap for more steps Cancel the common factor of
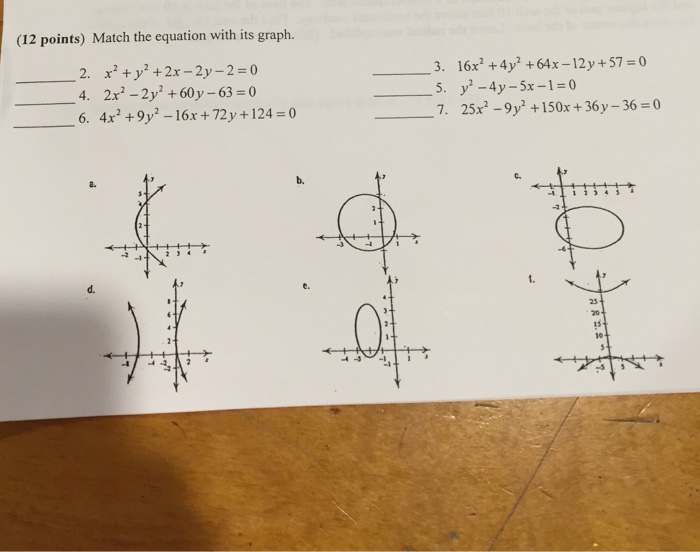



Match The Equation With Its Graph 2 X 2 Y 2 Chegg Com




Find The Volume Of The Region The Solid Bounded By X 2 2y 2 2 Z 0 X Y 2z 2 Study Com
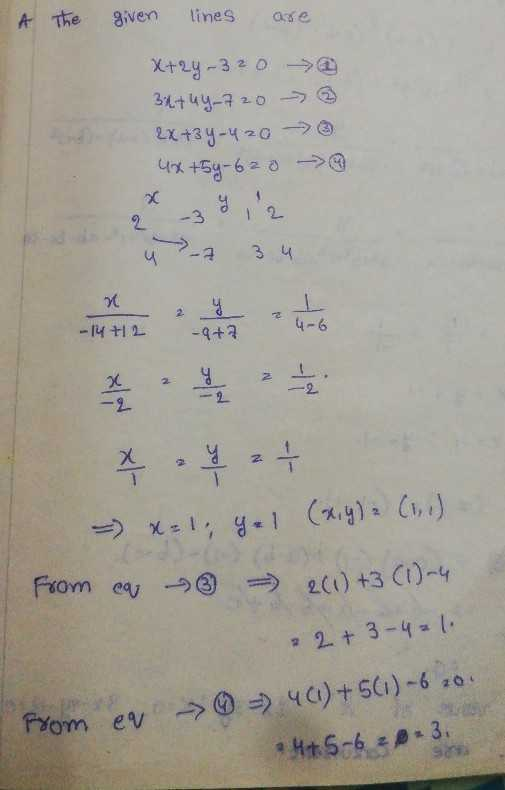



Check Whether The Pair Of Equations X 2y 0 And 3x 4y R Scholr




Splash Screen Ppt Download
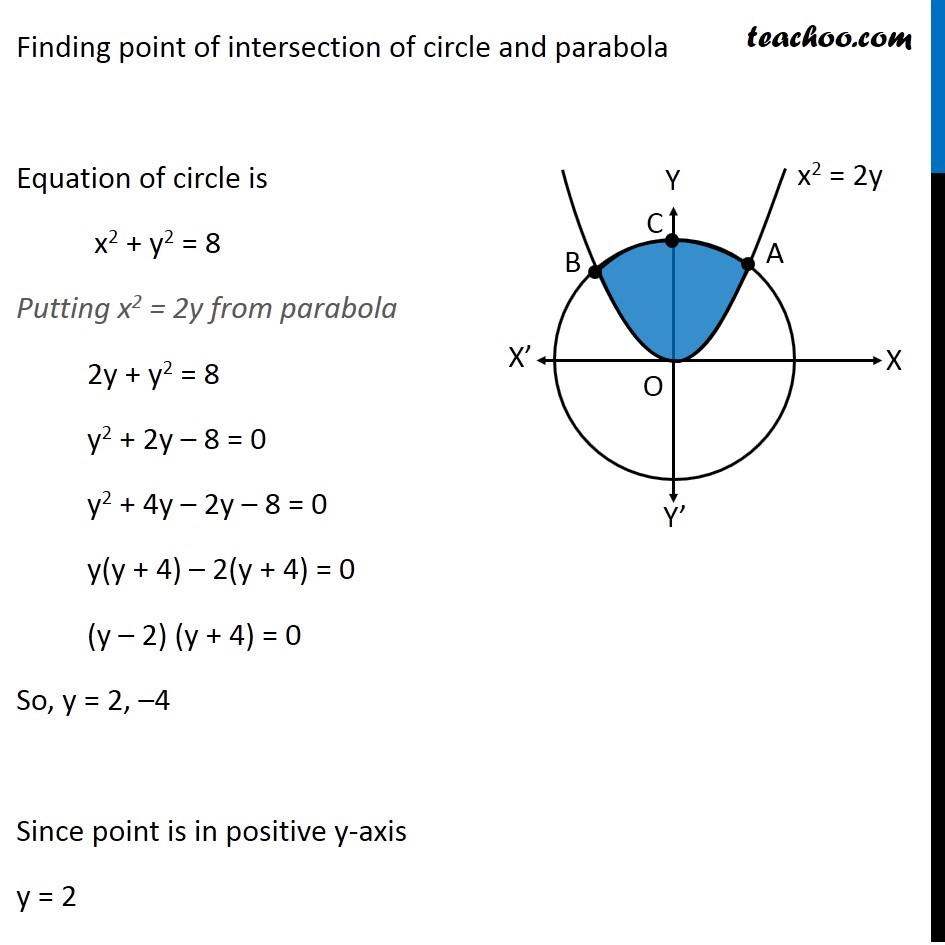



Find The Area Of The Region X Y X 2 Y 2 8 X 2 2y




Graphical Method Of Solution Of A Pair Of Linear Equations Ck 12 Foundation




A Circle Has The Equation X 2 Y 2 2x 2y 2 0



X 2 Y 2 2x 8y 8 0 Mathskey Com



Solution I Need Help Graphing X 2 Y 2 2x 2y 2 I Also Need To Find The Intercepts



Draw The Graphs Of The Pair Of Linear Equations X 2y 5 And 2x 3y 4 Also Find The Points Where The Lines Meet The X Axis Sarthaks Econnect Largest Online Education Community



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
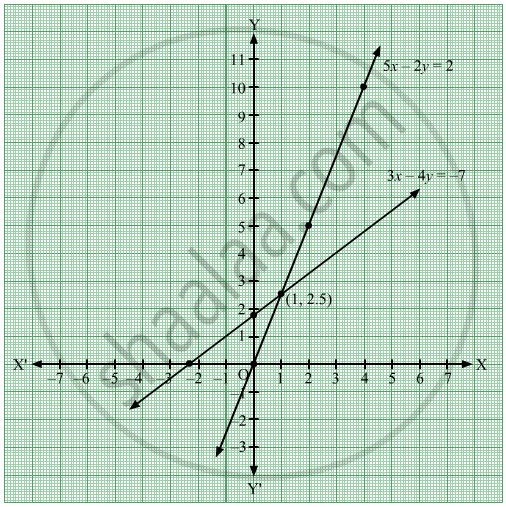



Solve The Following Simultaneous Equations Graphically 3x 4y 7 5x 2y 0 Algebra Shaalaa Com




The Equation Of A Circle Is X 2 Y 2 4x 2y 11 0 What Are The Center And The Radius Of The Brainly Com




X 2 Y 2 2y 0 Graph Novocom Top
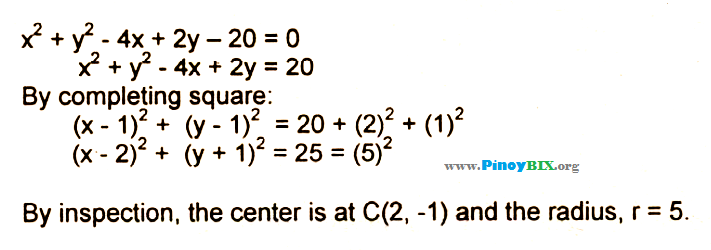



Solution The Equation X 2 Y 2 4x 2y 0 Describes



Solution Graph Linear Equations Give X And Y Intercepts 2x Y 2 3x 2y 6 3x 2y 0




Ex 6 3 12 Solve Graphically X 2y 3 3x 4y 12



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf



Let C 1 X 2 Y 2 2x 2y 0 And C 2 X 2 Y 2 2x 2y 0 Are Two Given Circles From A Mov Youtube



Graph Graph Equations With Step By Step Math Problem Solver



Introduction 1 Page 1




Solution The Equation X 2 Y 2 4x 2y 0 Describes



Find The Area Of The Region X Y X 2 Y 2 8 X 2 2y




Warmups Solve Using Substitution Ppt Download




X 2 Y 2 2y In Polar Form



Q Tbn And9gctwl8ksal48ks9fvcggchq7ifw Mt5nzxx1 0ivsjobxia io Usqp Cau
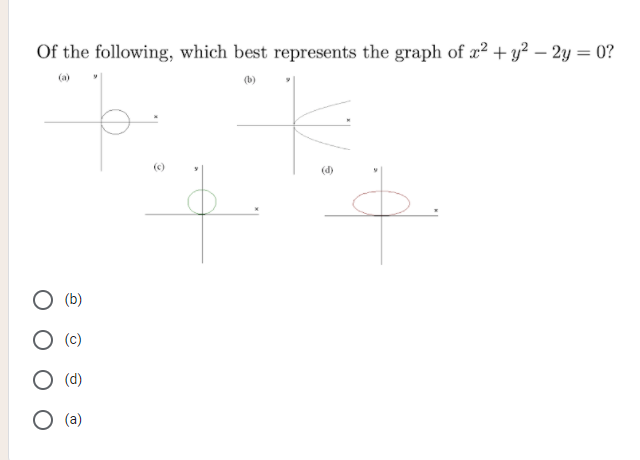



Solved Of The Following Which Best Represents The Graph Chegg Com
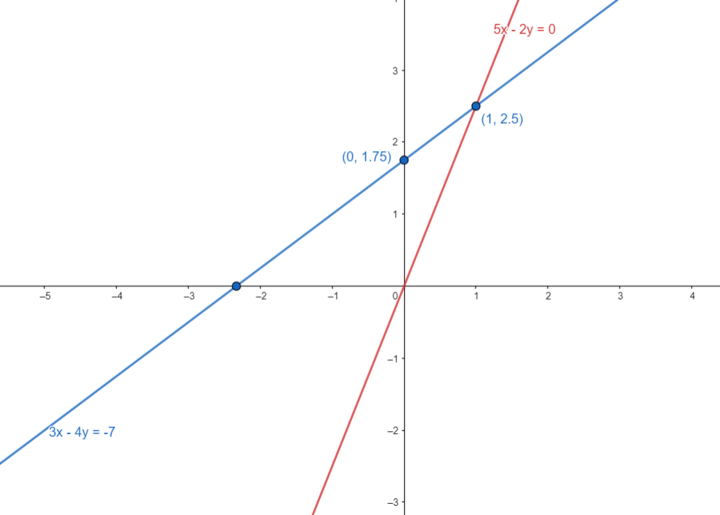



Q2e 3x 4y 7 5x 2y 0 Solve The Following Simultaneous Equation Graphically
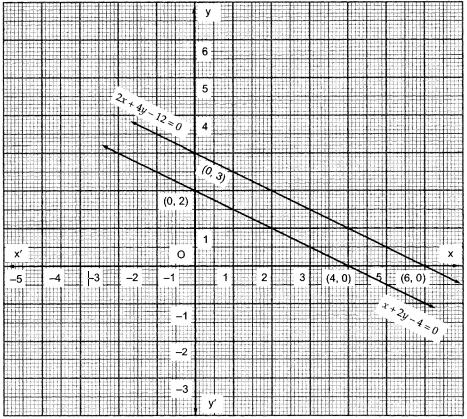



The Path Of A Train A Is Given By The Equation X 2y 4 0 And The Path Of Another Train B Is Given By The Equation 2x



Www Topperlearning Com Answer 1draw The Graph Of The Equation X 2y 0 2draw The Graph Of Each Of The Equations 2x 3y 5 0 And 5x 4y 1 0 And Find The Coordinates Of The Point Where Th 9icvp4qq




X 2y 0 3x 4y Draw In Graph Homework Help Mycbseguide



How Do We Graph The Equation X 2 Y 3 1 What Is The Slope Quora
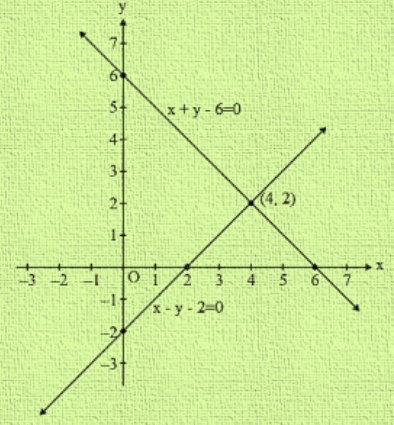



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2



How Do You Solve 3x 2y 0 And 3x Y 18 By Graphing Socratic




Solve Graphically X 2y 0 3x 4y 0 Brainly In
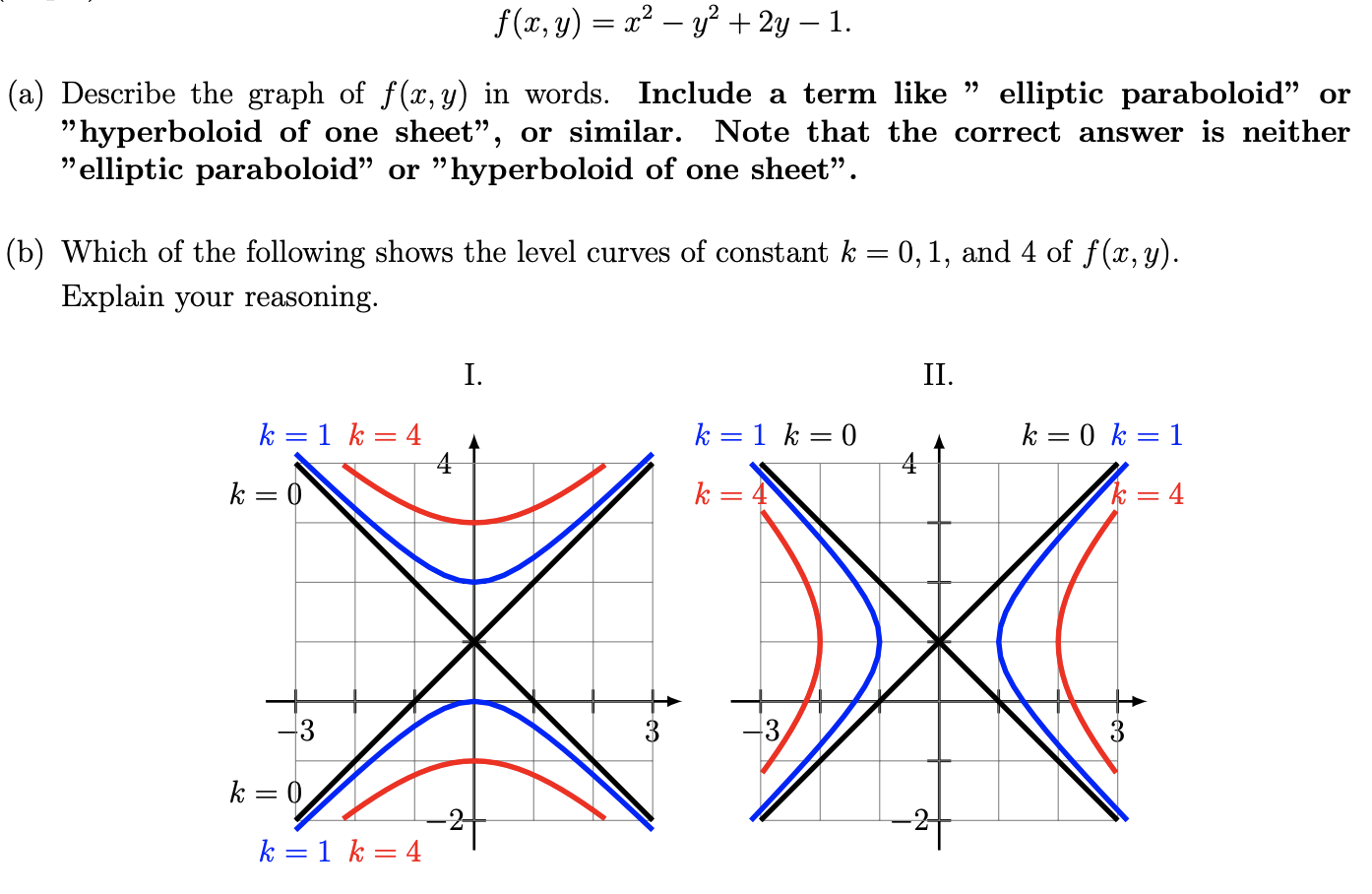



Let F X Y X 2 Y 2 2y 1 A Describe The Chegg Com




How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange




How Do You Graph X 2 Y 2 4 Socratic




Lii06 Ppts 0302
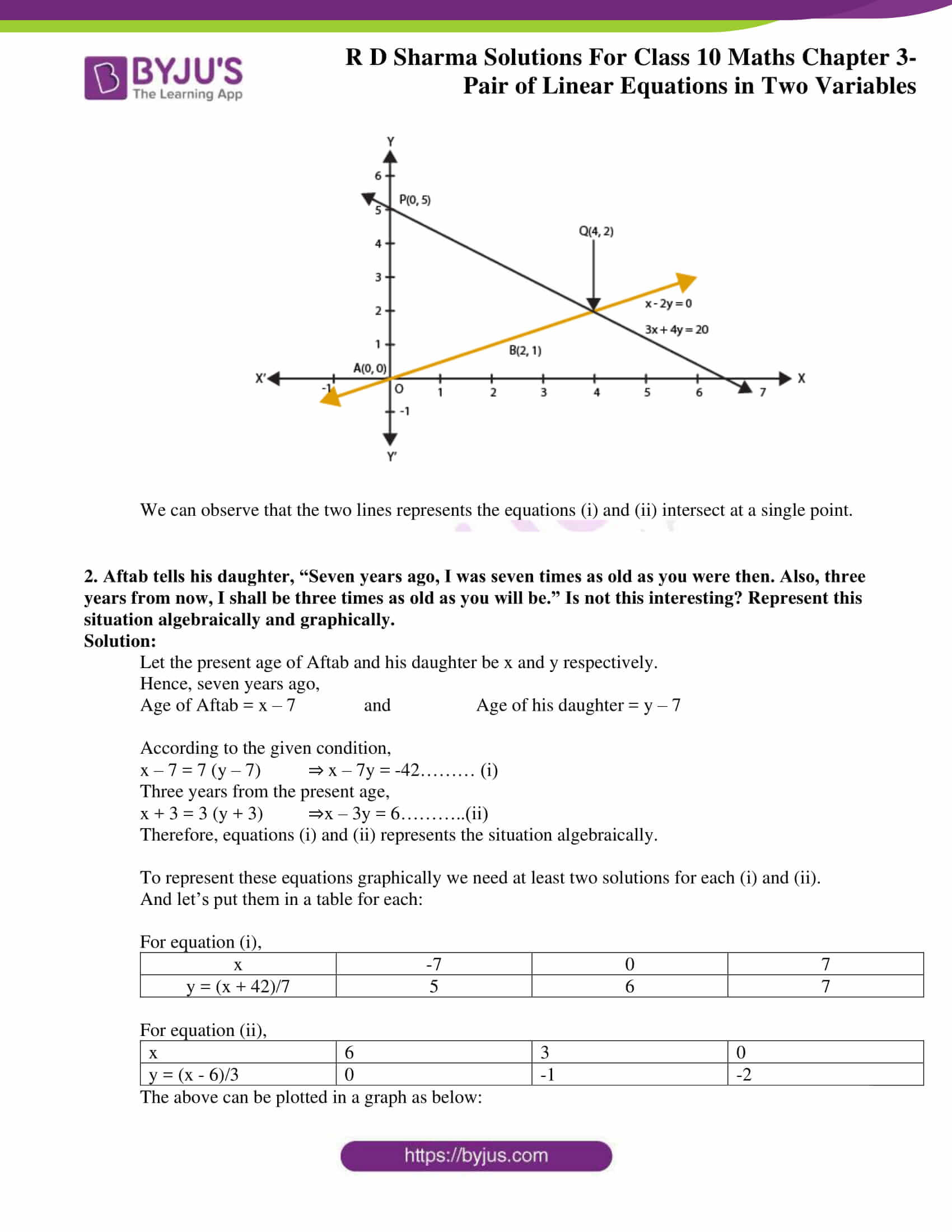



Rd Sharma Solutions For Class 10 Chapter 3 Pair Of Linear Equations In Two Variables




Solve The System Of Equations By Graphing X 2y 0 X Y 6 Ppt Video Online Download




How To Find The Volume Of The Region Bounded By Math X 2y Y 2 Math Math X 0 Math Revolving About The X Axis Using The Shell Method Quora




Plotting All Of A Trigonometric Function X 2 Y 2 1 With Matplotlib And Python Stack Overflow




Draw A Graph Of A Equation X Y 5 And 3x 2y 0 On The Same Graph Paper Find The Coordinates Of The Point Brainly In
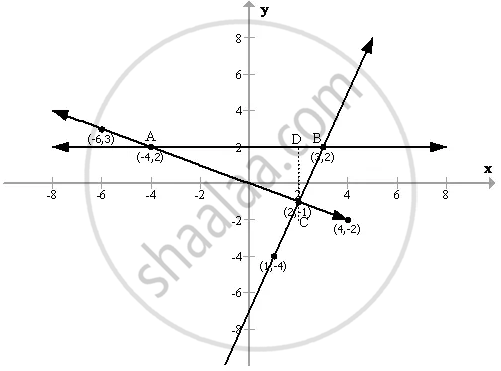



The Sides Of A Triangle Are Given By The Equations Y 2 0 Y 1 3 X 2 And X 2y O Find Graphically The Area Of Triangle Mathematics Shaalaa Com




Systems Of Equations With Graphing Article Khan Academy



Draw The Graph Of The Equation X 2y 4 Use Graph To Find



1
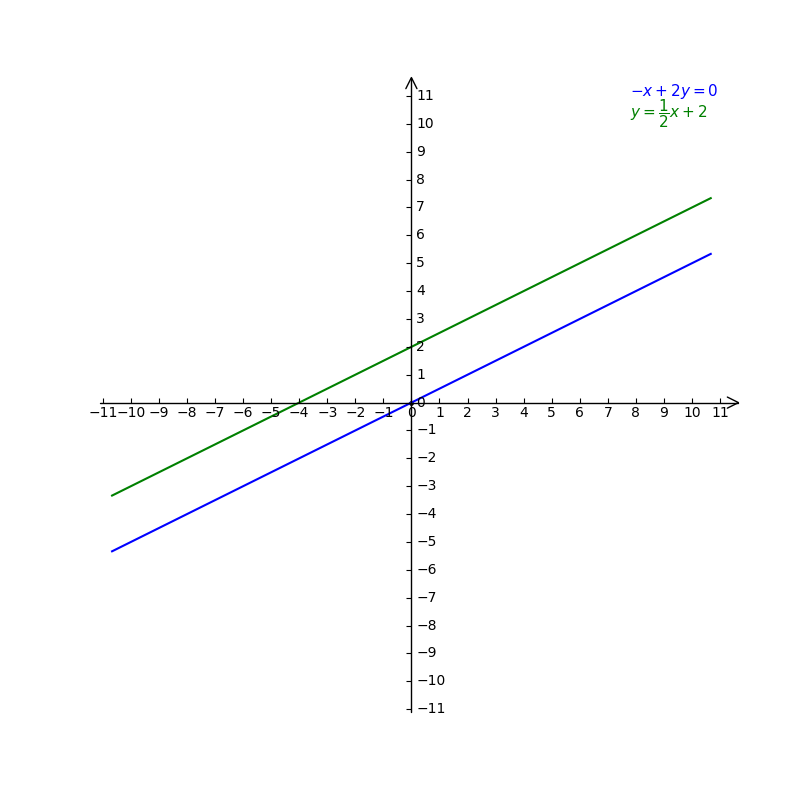



Graph The System Below And Write Its Solution B Gauthmath



Draw The Graph Of Two Lines Whose Equations Are 3x 2y 6 0 And X 2y 6 0 On The Same Graph Paper Sarthaks Econnect Largest Online Education Community




Draw The Graph Of The Equation X Y 5 And 3x 2y 0 On The Same Graph Find The Cordinates Of The Point Where Maths Meritnation Com




Answered Linear Equations 26 Chapter 1 Problems Bartleby




Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Youtube
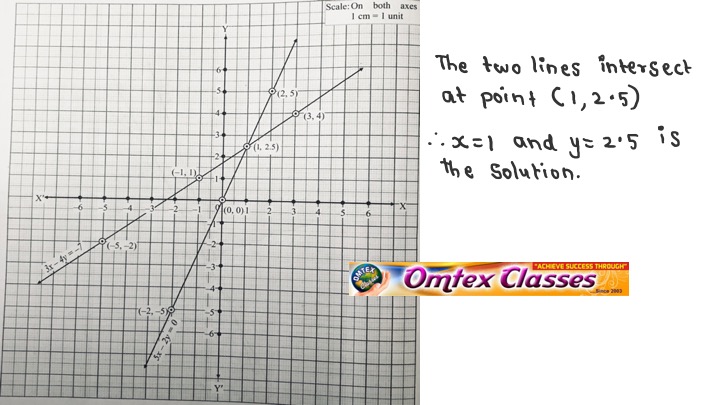



Omtex Classes 3x 4y 7 5x 2y 0 Solve The Following Simultaneous Equations Graphically



Graph Graph Equations With Step By Step Math Problem Solver




X 2 Y 2 2y 0 Graph Novocom Top




X 2 Y 2 2y 0 Graph Novocom Top



Solution Graph The Equation Y 2x 0 And X 2y 0 Where Do These Graphs Intersect




Plotting X 2 Y 2 1 3 X 2 Y 3 0 Mathematics Stack Exchange
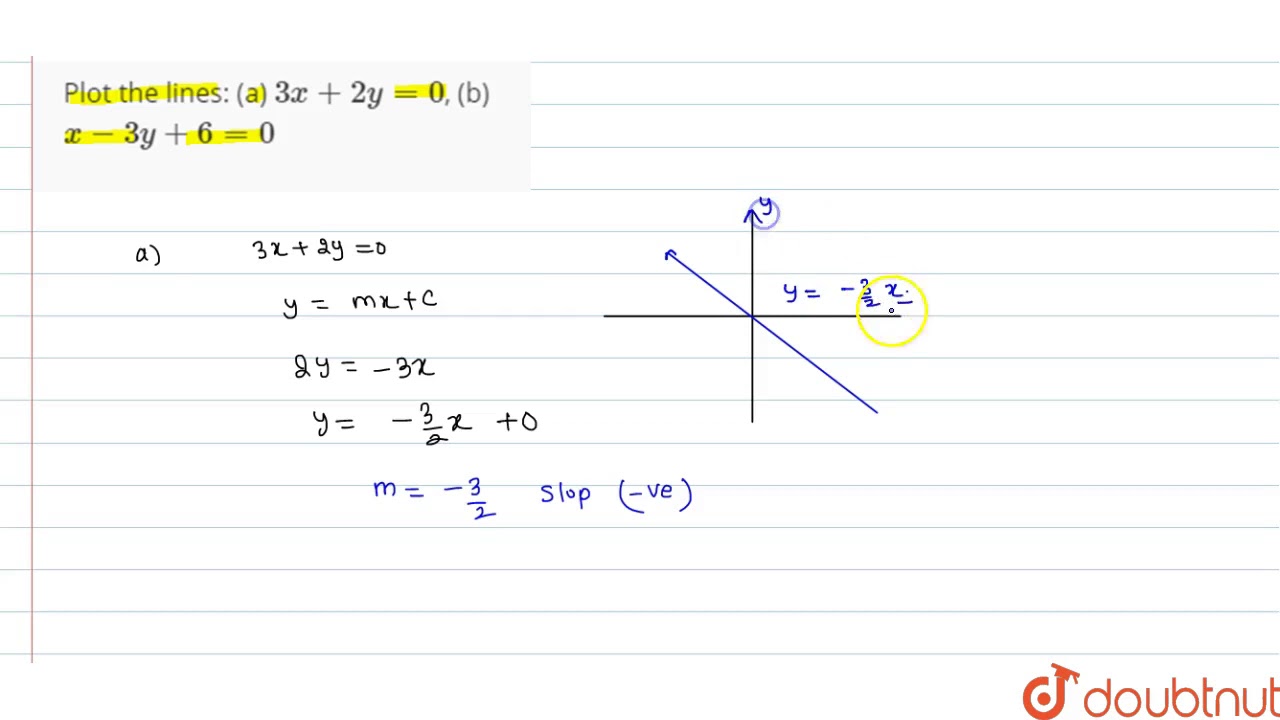



Plot The Lines A 3x 2y 0 B X 3y 6 0 Youtube



Graphinglines
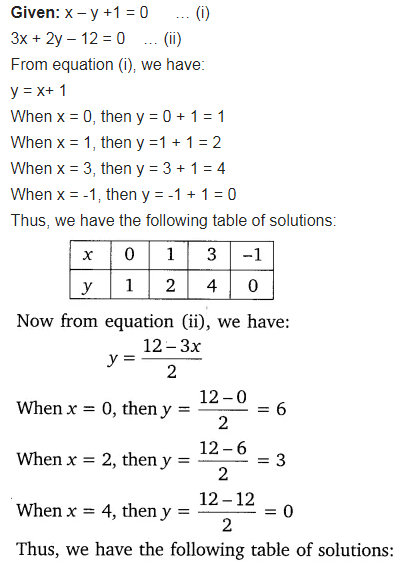



Draw The Graphs Of The Equations X Y 1 0 And 3x 2y 12 0 Cbse Class 10 Maths Learn Cbse Forum




Sketch The Region Bounded By The Graphs Of The Equations X Y 2 2y X 1 Y 0 Study Com




R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
.png)



Draw The Graphs Of 3x 2y 0 And 2x 3y 0 What Is The Oint Of Intesection Of The Two Lines Representing The Maths Meritnation Com




Which Of The Following Could Be The Graph Of The Chegg Com




X 2 Y 1 Is A Solution Of The Linear Equation A X 2y 0
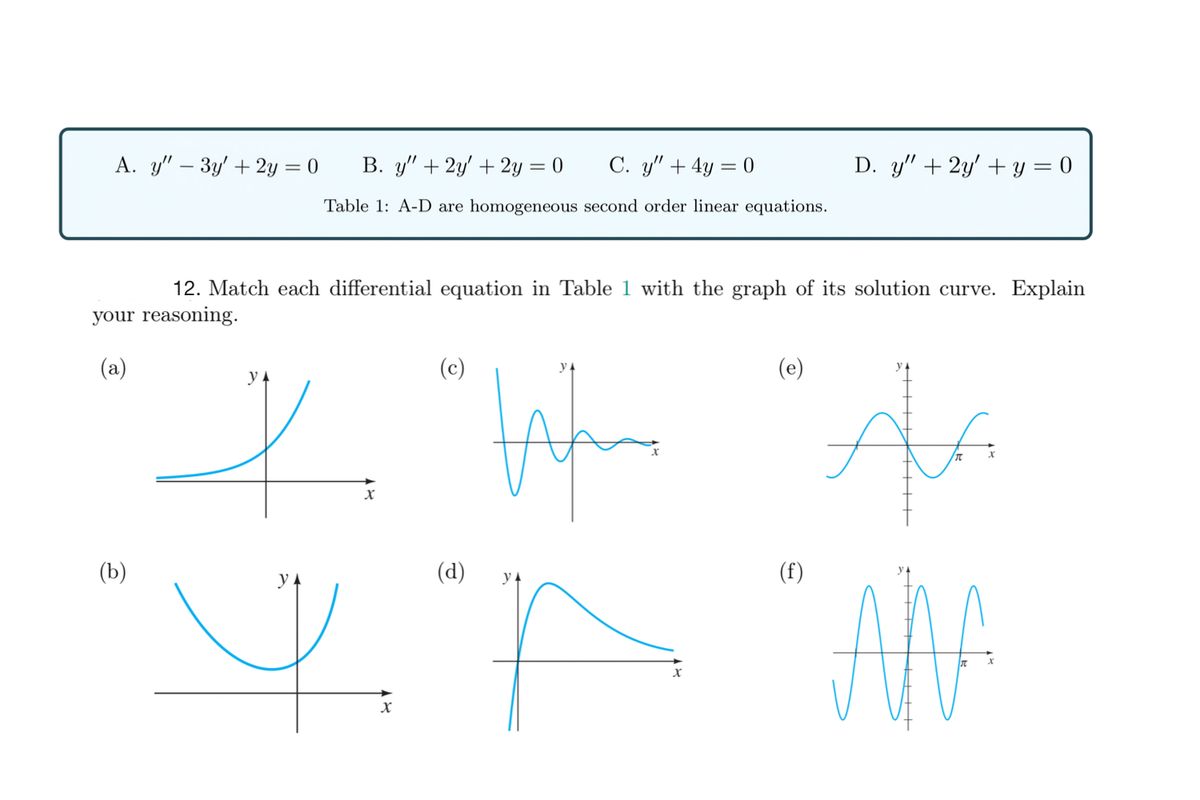



Answered A Y 3y 2y 0 B Y 2y 2y Bartleby



Draw The Graphs Of The Following Equations 2x Y 1 X 2y 13 Find The Solution Of The Equations From The Graph Sarthaks Econnect Largest Online Education Community




Draw The Graph Of The Equation X 2y 0 Brainly In




How Should I Draw Graph Of Math X 2 Y 2 0 Math The Radius Is Zero What Should I Do Quora




Ex 3 2 4 Which Of The Pairs Of Linear Equations Are Ex 3 2




X 2 Y 2 2y 0 Graph Novocom Top




Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy



1




Through Which Quadrants The Graph Of The Linear Equation X 2y 0 Will Pass Maths Linear Equations In Two Variables Meritnation Com




Surfaces Part 2



Ellipses And Hyperbolae




Ex 6 3 5 Solve 2x Y 1 X 2y 1 Graphically Ex 6 3




Graph Of X 2y 0 Novocom Top



0 件のコメント:
コメントを投稿