三角形の1つの外角 → 赤色の外角 のこと; 基本的に、三角関数の角度は 半径 \(1\) の「単位円」 を利用して求めることができます。 単位円 \(1\) 周分の角度は、度数なら \(\color{red}{360^\circ}\)、ラジアンなら \(\color{red}{2\pi}\)直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と角度 斜辺と高さ 斜辺と角度 高さと角度 面積と底辺 面積と高さ 面積と斜辺 面積と角度
直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋
三角 角度 求め方
三角 角度 求め方- 三角定規 イラストや三角定規の角度のフラッシュカードです。 2つの三角定規の角度の足し算、引き算の学習にぴったりです。 繰り返しカードで学習することによって頭の中に 図形のイメージができ苦手意識がなくなります。 角度の求め方 算数の教え三角比の定義 sinθ= y r cosθ= x r tanθ= y x この定義により,辺の長さは,次のように表せる。 y = rsinθ x = rcosθ y = xtanθ 30◦, 45◦, 60◦の三角比は,下の図から求められる。 sin30◦= 1 2 cos45 = 1 √ 2 tan60 = √ 3 1 = √ 3 問 下の表を完成せよ。 θ 30◦45◦60◦




角度の求め方 角度の求め方 Mqttk
・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。 sin(サイン)から角度 cos(コサイン)から角度頂角の求め方、二等辺三角形との関係 頂角の求め方を下式に示します。 頂角=180°-2×底角 三角形の内角の和は180°です。2つの底角の角度は等しいので180°から底角の2倍を引いた値が頂角となります。 下図の二等辺三角形の頂角を求めてください。三角関数の角度は「三角関数の逆関数」を求めることで算定できます。 三角関数y=sinθについて、θ=の形になるような関数を「アークサイン(Arcsin)」といいます。 例えばsin (π/2)=1のとき、逆関数をとるとArcsin (1)=π/2≒157(≒90°)となります。 よって「sinθ=035」のようにθが未知数の場合、アークサインをとることでθを逆算できます。 今回は三角関数の角度の
という使い方に限られるわけではありません。 余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、「右辺は辺の長さだけ」でできており、左辺は角度だけでできています。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでaの角度は、360°(72°38°30°)=2° よって、 答え a=2 ° 角度③ 応用問題 例題4 1組の三角定規を下の図のように重ねました。この図でaの角度は何度になるか求めなさい。 三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135° x=135°-60°=75°
三角形の角度 無料で使える中学学習プリント 三角関数の基礎角度の求め方とは? (sinθ=1/2からθを計算 三角形の面積の求め方まとめ。 タイプ別でわかる公式一覧 三角形の面積は「 \ (底辺×高さ÷2\) 」という公式から求まりますが、この公式以外三角形、四角形、角、面積 円、三角形、四角形の面積を計算できるようになろう。 角度のはかり方もいっしょにおぼえてね。 動画で学ぼう! (NHK for School) 三角形の面積の求め方を、四角に直すことで原理から考える。 結婚式場から指輪が盗まれた 以上をまとめると三角方程式の解き方は「 単位円 を描き、 y=aの直線 を加えて、 三角形の比 を求めて角度を求め、 範囲を確認 して当てはまるもののみ答える」となります。 また、三角形の比は有名角のもの(30°、45°、60°など)に限られます。
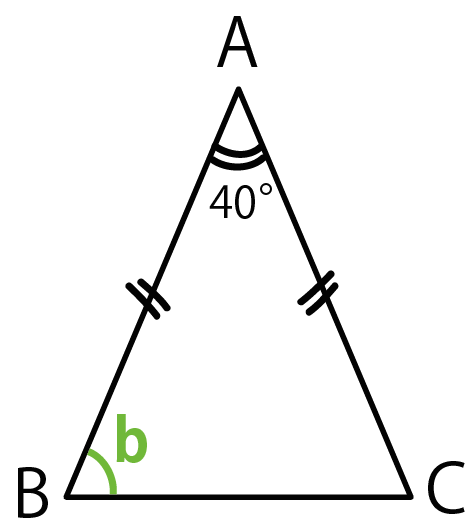



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋
三角比からの角度の求め方3(tanθ) step1 ポイント 三角比からの角度の求め方3(tanθ) 高校数学Ⅰで学ぶ「三角比からの角度の求め方3(tanθ)」のテストによく出るポイントを学習しよう! step2 例題 三角比からの角度の求め方3(tanθ) 高校数学Ⅰでだから、 外角の大きさ = ★ ってこと! ホント・・??じゃあ、この三角形の外角を求めてみよう! 外角の求め方① 40°75°∠x=180° → ∠x=65°三角形の内角と外角の関係から ● = ○ + ● 角A=30°+90°=1°
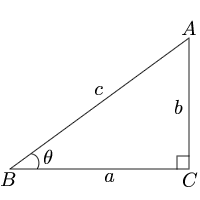



三角関数から角度 逆三角関数 三角形の計算 計算サイト




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo
解説 三角比というのは,与えられた角度に対して,ただ1つ値が決まるもので,その角度が「どんな形の三角形の角の大きさであるか」にはよらないからです。 この話を考えるとき,三角比の 「値を求める」 のか, 「値を利用する」 のかを区別して考えてみましょう。星形の角度の求め方を解説! ブーメラン型の角度の求め方! ちょうちょ型の角度の求め方を解説! 合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法! 証明の書き方合同な三角形の証明問題の書き方を基礎から解説!三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




あ かまでの角度を求めてください 急いでます 教えてください Clear
単位円を使って、一般の角度θについても三角関数を定義できます。 実務で使うなら、上の定義で十分でしょう。 三角関数の使い方1(角度から長さを求める) 例題:50cmのアームの一方を固定して、地面との角度が40°になるまで持ち上げたとき、正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりままずは、角度Bは簡単に求まります。三角形の内角の和は180度ですから、「C = 180 A B = 180 35 90 = 55」より、角Cの大きさは55度だと分かります。 aとbの求め方 次に、aとbを求めてみましょう。 三角関数の定義から、「a = c sin A = 7×sin35°」、「b = c cos A = 7×




角度の求め方 算数の教え上手 学びの場 Com



円と三角形 角度 中学から数学だいすき
三角形の内角の和は \(180°\) より、\(∠bad=180°∠abd∠adb\) これら4つの式を繋げると \(∠BAT=∠ACB\) となり、接弦定理を証明できました。/ 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c, sinθ= b c, tanθ= b a (2) P ythagorean theorem a2b2 =c2 R 同じように \(x\) 軸から測った角度 \(\theta\) の三角比はその点の座標になります。 三角比の値がマイナスになりますがこれは自然な三角比の拡張です。これが単位円を使った三角比の考え方でした。 では 180 度より大きくなっても大丈夫でしょうか。




高校数学 三角比からの角度の求め方3 Tan8 映像授業のtry It トライイット




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット
三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦(cos(コサイン))を求める。




三角形の外角と内角の公式 簡単な問題で 外角の求め方を理解しよう 中学や高校の数学の計算問題



日曜大工で使う数式



三角関数をマスターしよう その2 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習



三角関数 1 Cg 数学 06aa




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




小5 算数 小5 31 三角形の角 Youtube




Javaでmathクラスを使って三角関数を求める方法を現役エンジニアが解説 初心者向け Techacademyマガジン




タンジェントとは何か 中学生でも分かる三角関数の基礎



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト




三角形の角度を求める問題 小学生 中学生の勉強




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
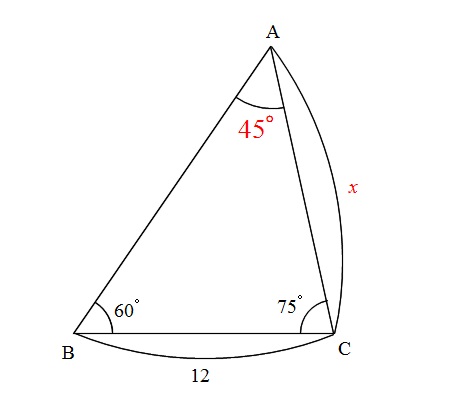



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典




高校数学 三角比からの角度の求め方2 Cos8 映像授業のtry It トライイット



二等辺三角形の公式 面積 高さ 角度 斜辺と周囲の長さ 数学 エクセルマニア




黄金三角形による18 シリーズの三角比 おいしい数学




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算




三角形面積求め方 三角形とは 面積公式 角度 辺の長さ 重心 比の計 Jbqhd




角度の求め方 角度の求め方 Mqttk
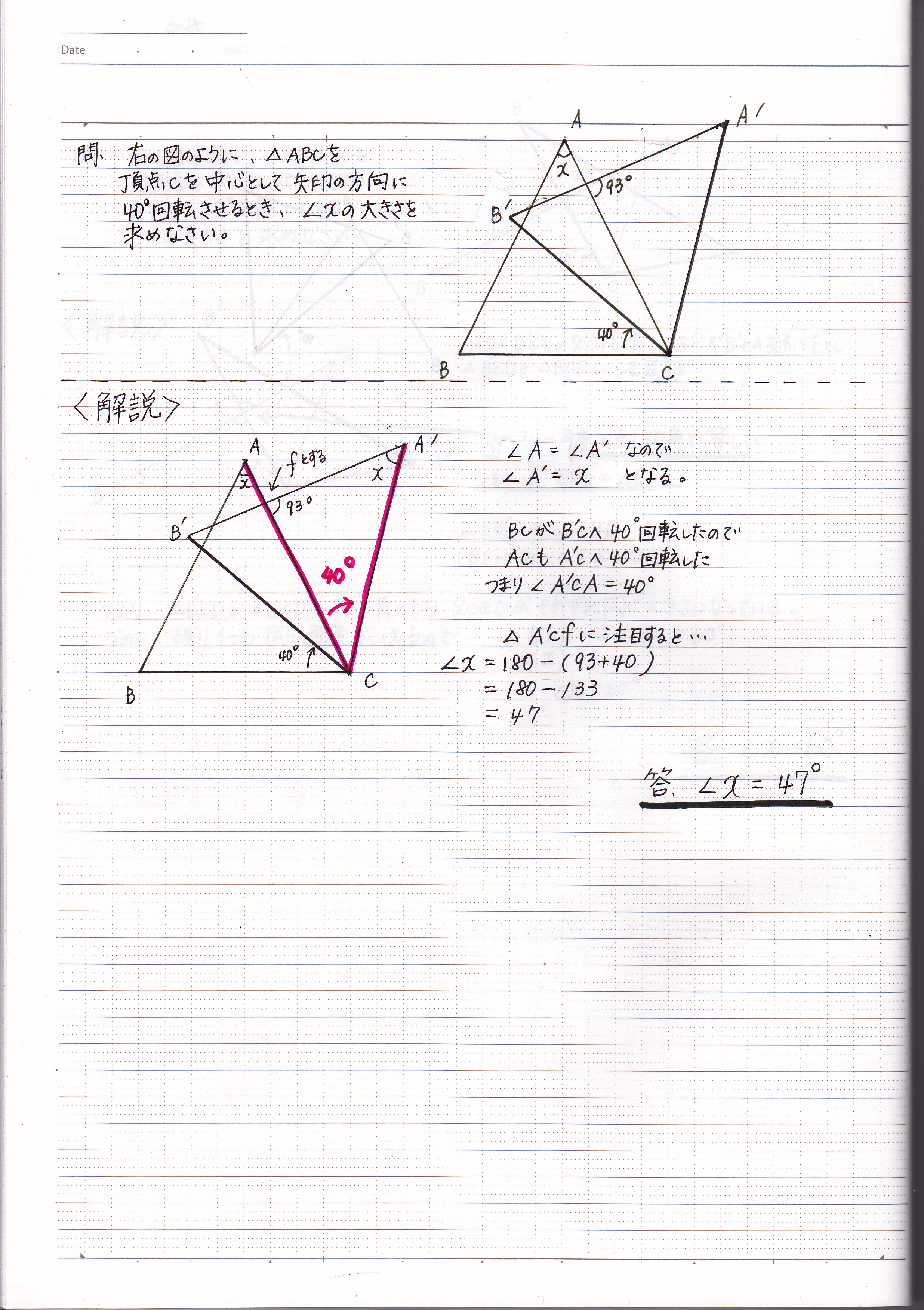



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方
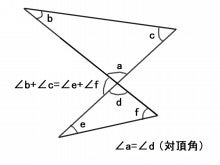



角度の求め方 数学が嫌いなんです
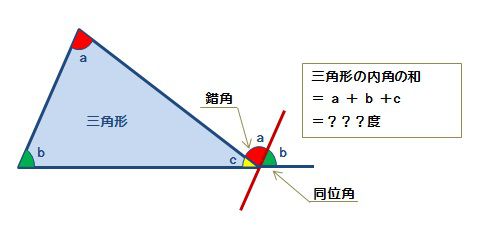



三角形の内角の和 算数の公式覚えてますか




黄金三角形による18 シリーズの三角比 おいしい数学




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




三角形の角度を求める問題 小学生 中学生の勉強




中2 数学 4 2 三角形の角度の利用 Youtube
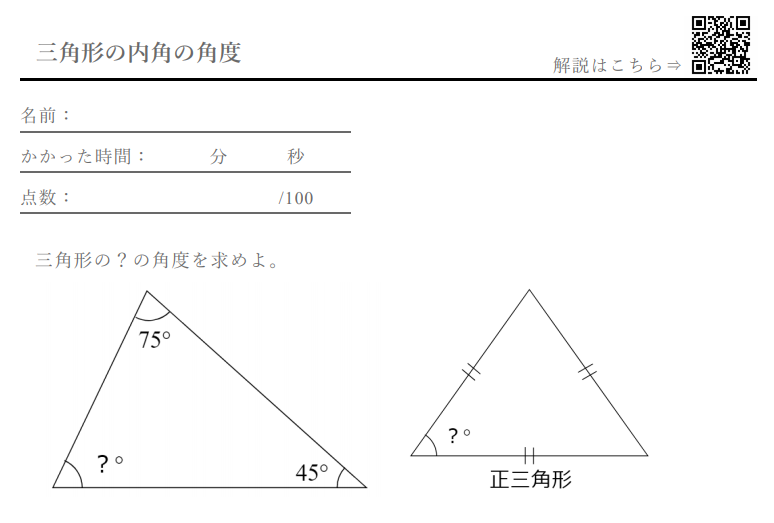



三角形 の内角の角度 計算ドリル 問題集 数学fun




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




底辺と高さから角度と斜辺を計算 高精度計算サイト



紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す



1
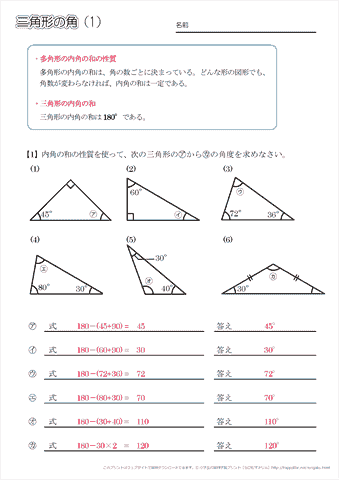



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信



1



直角三角形の解法 1




二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思うので教え Clear




角度の問題まとめ 無料で使える中学学習プリント




余弦定理で角度を求める方法 数学の星




算数 小4 9 角の大きさ 三角じょうぎ Youtube
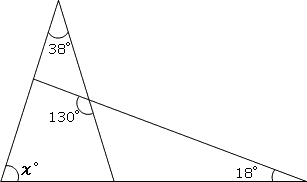



角度の求め方 算数の教え上手 学びの場 Com
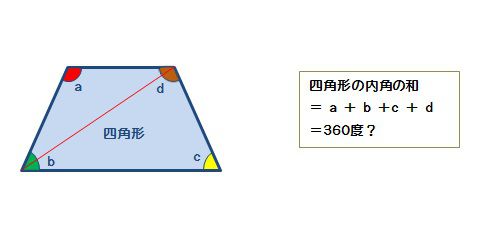



四角形の内角の和 算数の公式覚えてますか



直角三角形の解法 1
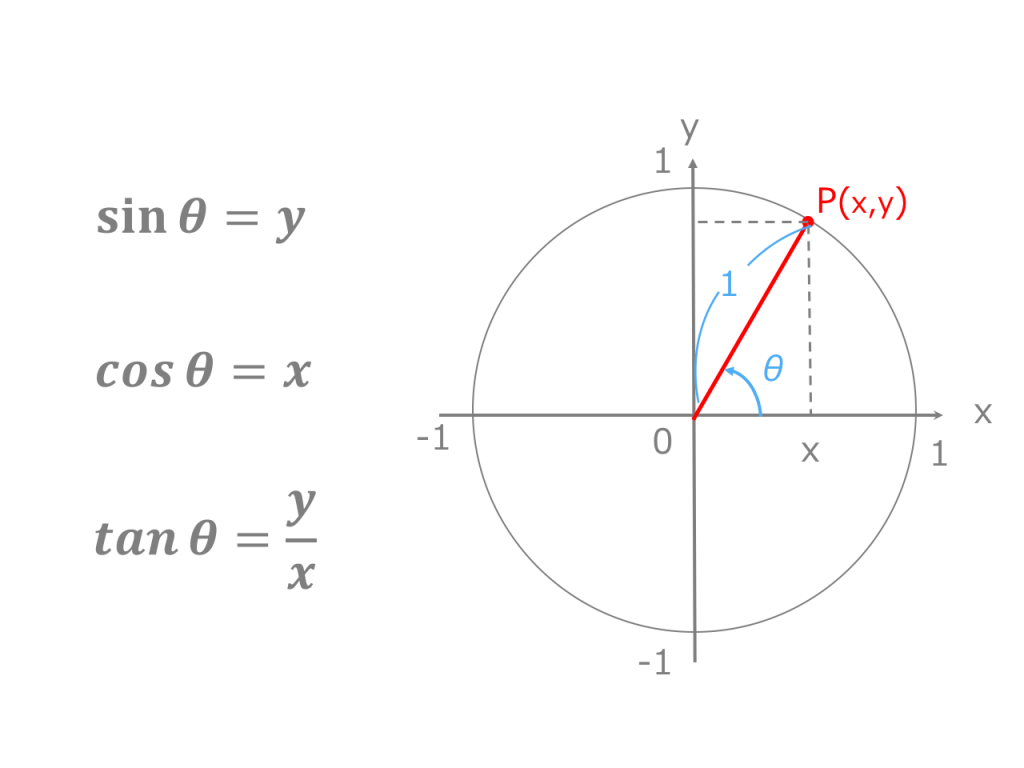



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
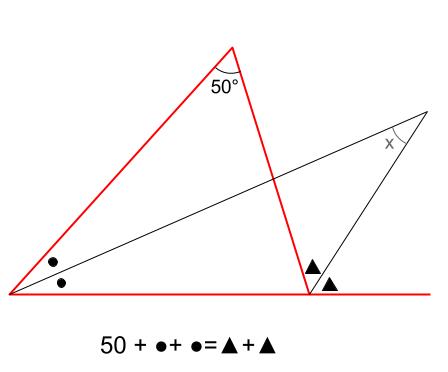



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su
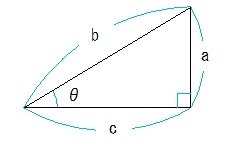



三角関数 ncプログラム基礎知識




小学校の算数で 三角じょうぎの角の大きさについて習います ここでは 2枚1組の三角定規をいろいろに組み合わせて できる角の大きさを 計算で求める自主学習ノートの例をご紹介します 学習ノート 学習 算数のアクティビティ




力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に




三角錐の稜線の角度の出し方 新米板金加工業者です 建築板金で三角 数学 教えて Goo




三角形の辺から角度を計算 製品設計知識




三角定規の角の大きさを確認し いろいろな図形の角度を計算で求める家庭学習ノートの例を紹介します 三角定規の角の大きさを確認 図形の角度を計算で求める 線が交わる時の角度 平行四辺 学習ノート 学習 小学校 算数




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学
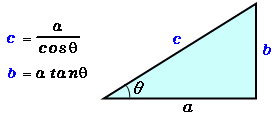



角度と底辺から斜辺と高さを計算 高精度計算サイト
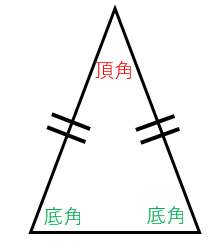



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学
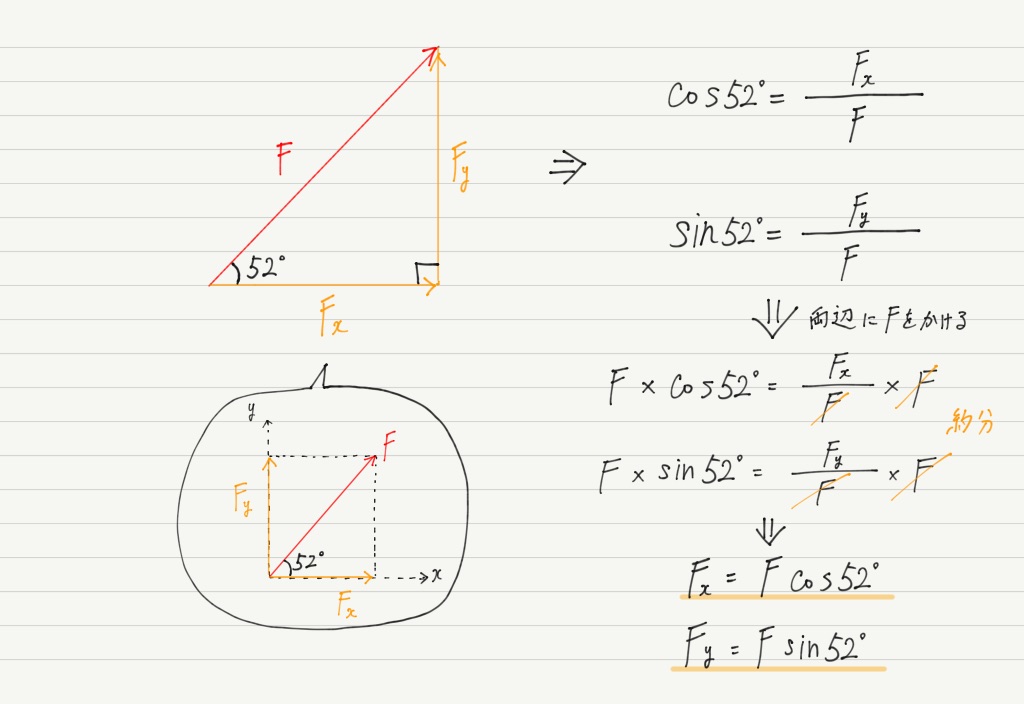



力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に




正三角形や二等辺三角形の内角 Youtube
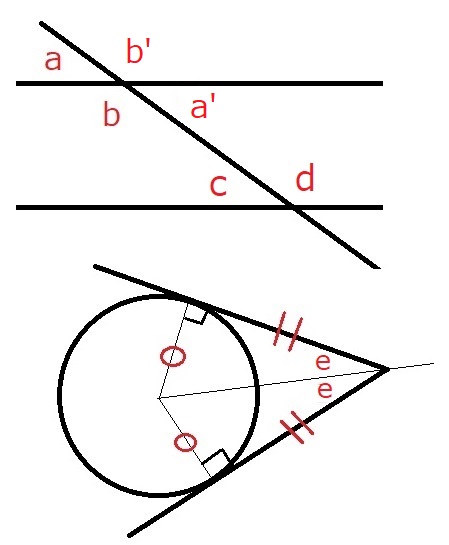



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




二等辺三角形の角を求める Youtube




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
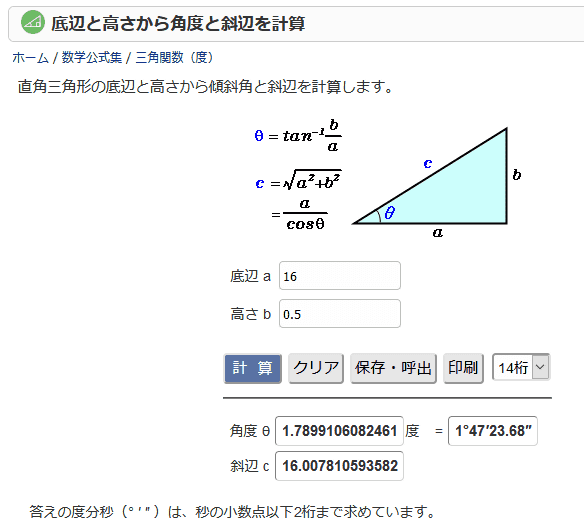



表計算ソフトを使って 底辺 と 高さ から 角度 を求める




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
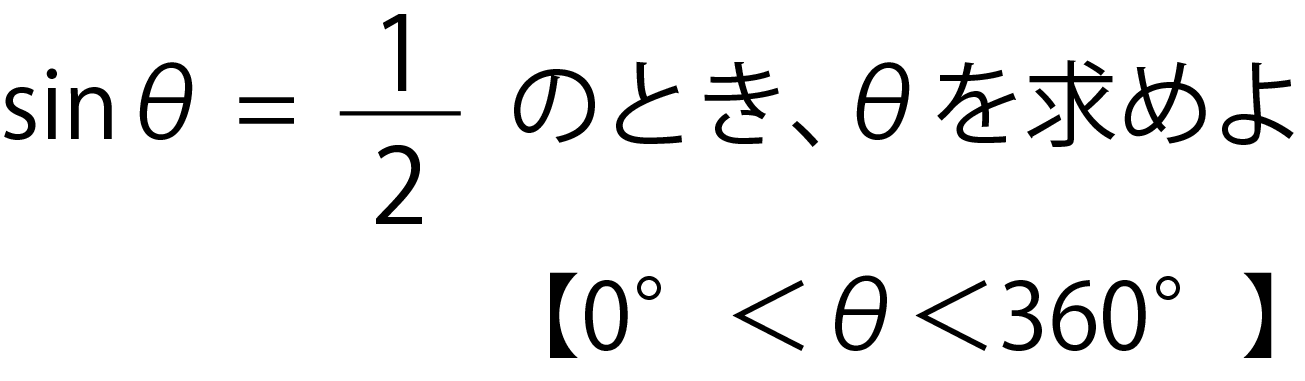



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




角度の求め方 算数の教え上手 学びの場 Com




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく
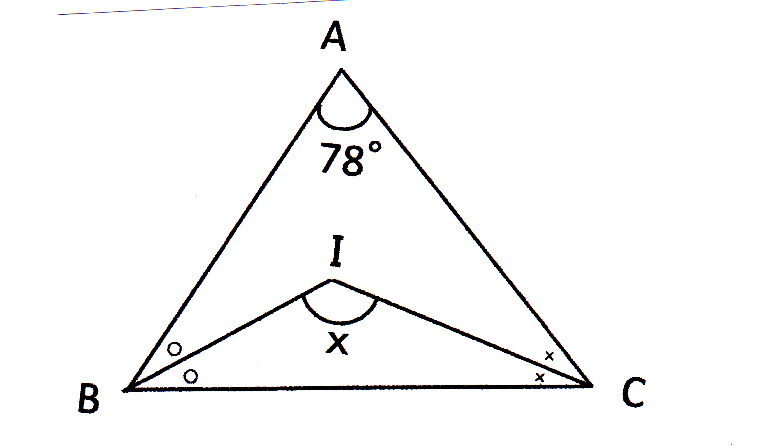



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



1



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明




重なり合う三角定規を使った角度の計算問題 小4 小5の算数 きいとこ




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座



三角形の角度を求める 思考力を鍛える数学
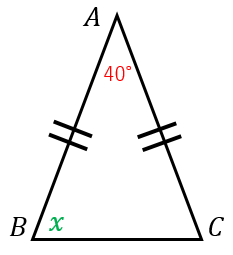



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学



内接円 内心




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




直角三角形公式角度 直角三角形 斜辺と角度 三角形の計算 計算サイト翻譯此網頁 Rzcpe
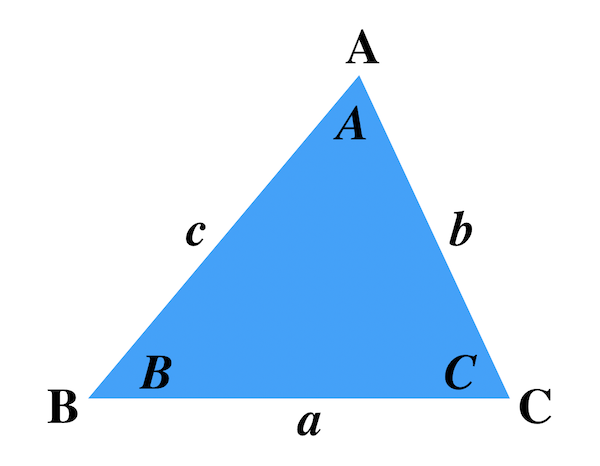



三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局
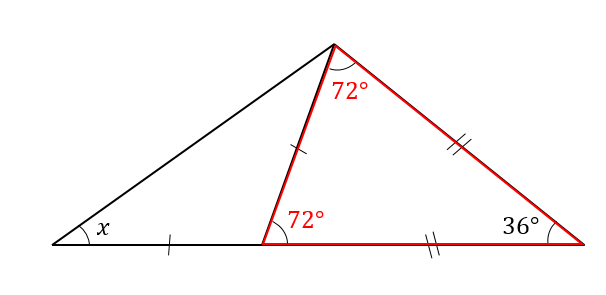



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




三角形の3辺から角度を計算 高精度計算サイト



3



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係



内接円 内心
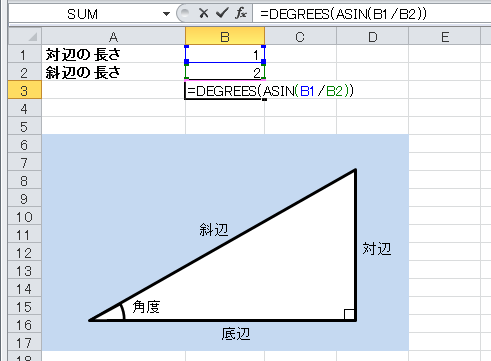



サインから角度を計算するには Asin Degreesの解説 エクセル関数リファレンス



0 件のコメント:
コメントを投稿